Римские цифры от 1 до 20
Содержание:
- Порядковые
- Принятие в Европе
- Простой принцип расчета
- Откуда взялись современные числовые знаки от 1 до 10
- Как написать римские цифры на клавиатуре
- Типографские варианты
- Японские числа от 1 до 10
- Часть 2. Преобразование буква — цифра.
- Часть 3. Реконструкция событий.
- Особенности арабской цифры 0 (ноль)
- Латинские буквы
Порядковые
| Первый | — | Про́тос |
| Второй | — | Дэ́фтэрос |
| Третий | — | Три́тос |
| Четвёртый | — | Тэ́тартос |
| Пятый | — | Пэ́мптос |
| Шестой | — | Э́ктос |
| Седьмой | — | Э́вдомос |
| Восьмой | — | О́кдоос |
| Девятый | — | Э́натос |
| Десятый | — | Дэ́катос |
| Одиннадцатый | — | Эндэ́катос |
| Двенадцатый | — | Додэ́катос |
| Тринадцатый | — | Дэ́катос три́тос |
| Четырнадцатый | — | Дэ́катос тэ́тартос |
| Пятнадцатый | — | Дэ́катос пэ́мптос |
| Шестнадцатый | — | Дэ́катос э́ктос |
| Семнадцатый | — | Дэ́катос э́вдомос |
| Восемнадцатый | — | Дэ́катос о́гдоос |
| Девятнадцатый | — | Дэ́катос э́натос |
| Двадцатый | — | Икост́с |
| Двадцать первый | — | Ико́стос про́отос |
| Тридцатый | — | Триакосто́с |
| Сороковой | — | Тэсаракосто́с |
| Пятидесятый | — | Пэндыкосто́с |
| Шестидесятый | — | Ксикосто́с |
| Семидесятый | — | Эвдомикосто́с |
| Восьмидесятый | — | огдоикостос |
| Девяностый | — | Энэникосто́с |
| Сотый | — | Экатосто́с |
| Двухсотый | — | Дъякосиосто́с |
| Трёхсотый | — | Триакосиосто́с |
| Тысячный | — | Хилиосто́с |
Принятие в Европе
Принятие индуистских цифр через арабов Европа
Woodcut показывая шестнадцатого века куранты из Упсалы собора , с двумя clockfaces, один с арабским и один с римскими цифрами.
Немецкая рукопись страница Обучение использование арабских цифр ( Талхоффер Thott, 1459). В это время, знание цифр прежнему широко рассматриваются как эзотерические и Талхоффер представляет их с древнееврейским алфавитом и астрологией .
В конце восемнадцатого века французский революционный «десятичный» циферблат.
В 825 Al-Хорезй написал трактат по – арабски, по расчету с индуистскими цифрами , который выживает только в качестве 12- го века латинского перевода, Algoritmi де Numero Indorum . Algoritmi , передача переводчика от имени автора, породила слова алгоритма .
Первые упоминания цифр на Западе встречаются в Codex Vigilanus 976.
Из 980s, Герберт из Орийака (позже, папа Сильвестр II ) использовал свое положение для распространения знаний о числительных в Европе. Герберт учился в Барселоне в молодости. Он , как известно, просил математические трактаты относительно астролябии от Люпитус Оф Барселона после того, как он вернулся во Францию.
Леонардо Фибоначчи ( Леонардо Пизанского ), математика родилась в Республике Пизы , изучавшая в Béjaïa (расширитель), Алжир , способствовали индийской системе счисления в Европе с его 1202 книгой Liber Abaci :
Цифры расположены с их низкой стоимостью разряда справа, с высшими позициями добавленной стоимости влево. Эта мера была принята тождественно в числительных, используемая в Европе. Языки, написанные на латинском алфавите хода слева-направо, в отличии от языков, написанных на арабском алфавите. Следовательно, с точки зрения читателя, числительные в западных текстах написано с наибольшей силой основания первой цифра в то время как арабские тексты написана с наималейшей мощностью основания первым.
Причина цифра более известна как «арабские цифры» в Европе и Америке является то , что они были введены в Европу в 10 веке арабских спикерами в Северной Африке, которые затем с помощью цифр из Ливии в Марокко. Арабы, с другой стороны, называют систему по основанию 10 ( а не только эти цифры) « индуистские цифры», обращаясь к их происхождениям в Индии. Это не следует путать с тем, что арабы называют “цифрами хинди”, а именно Восточное арабскими цифрами ( – 1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9 ) , используемые в Ближнем Востоке, или любые из цифр в настоящее время используется в индийских языках (например , деванагари : 0.1.2.3.4.5.6.7.8.9 ).
Европейская прием цифр была ускорена изобретением печатного станка , и они стали широко известен в 15 – м века. Рано свидетельствует об их использовании в Великобритании включает в себя: равен часовой хорарную квадрант из 1396, в Англии, в 1445 надпись на башне Heathfield Церкви, Сассекс>>Bray Церкви, Беркшир>>Piddletrenthide церкви, Дорсет>>Шотландии 1470 Надпись на могиле первого Графа Хантли в Elgin собора. (См GF Hill, The Development арабских цифр в Европе для большего количества примеров.) В центральной Европе, король Венгрии Ладислав Постум , начал использование арабских цифр, которые появляются впервые в королевском документе 1456. По в середине 16 – го века, они широко используются в большинстве стран Европы. Римские цифры остались в использовании в основном для обозначения Anno Domini лет, и для чисел на clockfaces.
Сегодня, римские цифры все еще используются для перечисления списков (как альтернатива к алфавитной нумерации), для последовательных томов, различать монарх или член семьи с теми же самыми первыми именами, и (в нижнем регистре) пронумеровать страницы в вступительных частях материала в книгах ,
Простой принцип расчета
Римские числа математически конвертируются в арабские числа путём простого назначения каждой цифре Римского числа соответствующего целочисленного значения в арабской системе с автоматическим суммированием: M=1000 | D=500 | C=100 | L=50 | X=10 | V=5 | I=1.
Ниже приводятся детальное описание всех основных римских цифр:
| Самый простой способ записать маленькие числа это нарисовать «зазубрины» — цифра один: I. Две палочки II означают два, III — три. Однако, для большего числа количество становиться очень большим и абсолютно не читаемым…. |
20-ый век1901 = MCMI 1902 = MCMII 1903 = MCMIII 1904 = MCMIV 1911 = MCMXI 1912 = MCMXII 1913 = MCMXIII 1914 = 1921 = MCMXXI 1922 = MCMXXII 1923 = MCMXXIII 1924 = 1931 = MCMXXXI 1932 = MCMXXXII 1933 = MCMXXXIII 1934 |
1941 = MCMXLI 1942 = MCMXLII 1943 = MCMXLIII 1944 = 1951 = MCMLI 1952 = MCMLII 1953 = MCMLIII 1954 = 1961 = MCMLXI 1962 = MCMLXII 1963 = MCMLXIII 1964 = 1971 = MCMLXXI 1972 = MCMLXXII 1973 = MCMLXXIII 1974 |
1981 = MCMLXXXI 1982 = MCMLXXXII 1983 = MCMLXXXIII 1991 = MCMXCI 1992 = MCMXCII 1993 = MCMXCIII 1994 = 2001 = MMI2002 = MMII2003 = MMIII2004 = MMIV2005 = MMV2006 = 2011 = MMXI2012 = MMXII2013 = |
|
| Таким образом, появилась число 5 — V. Расположение перед ним единички: IV — или расположение любого другого меньшего числа, чем последующий (в нашем случае символ пять) — означает вычитание. Таким образом, IV означает 4. После V можно указать меньшие цифры, тогда это будет означать складывание — VI означает 6, VII означает 7, VIII равно 8. | ||||
| X означает 10. Но что насчет 9? Аналогичное используется правило как с пятёркой. IX означает вычитание I из X, и это равно 9. Числа первого десятка, второго десятка и третьего формируются таким же образом, только с X-ами означающие количество десятков в числе. Таким образом, мы получаем, что XXXI — 31, а XXIV это 24. | ||||
| Значение L равно 50. Основываясь на том, что вы уже прочитали выше, вы уже можете догадаться, как будет записано число 40. Если вы думаете, что это будет XL, то вы правы = 10 отнимается от 50-и. И другие числа 60, 70, и 80 будут выглядеть как LX, LXX и LXXX. | ||||
| Цифра C пошла от слова centum, латинского слова означающее 100. centurion означает 100 людей. Мы по-прежнему используем такие слова, как «century» (столетие) и «cent» (цент). Как и с L, вычитание десятка означает понижение основной последующей цифры: 90 будет записано, как 100 минус 10 = XC. Несколько подряд цифр C будет означать соответствующее количество сотен: CCCLXIX равно 369. | ||||
| D указывает на значение равное 500. По аналогии, CD означает 400. CDXLVIII равное 448. | ||||
| M это 1000. Это цифра очень часто попадается, так как римские числа в основном используются для записи года. MMX — 2010 год. | ||||
| Более большие числа в Римском исчислении записываются при помощи горизонтальной линии расположенной над цифрами, что будет означать умножение данных цифр на тысячу. Отсюда выходит, что V с горизонтальной линией над этой цифрой будет означать 5000. |
Откуда взялись современные числовые знаки от 1 до 10
Зарождение арабских цифр относят к древней южной Индии. Во многих древних странах, когда еще не было письма, использовались для счета палочки. Одна палочка обозначала 1, две — 2 и так далее. Такой способ записи навеян зарубками. Именно отсюда и происходят числа в римском представлении (для цифр 1, 2, 3). Индийские цифры позаимствовали некоторые элементы буквы из разных стран того времени.
В цифрах встречаются признаки букв арамейского, греческого и финикийского алфавитов. Предположительно числовые знаки начали зарождаться во 2 веке до нашей эры, в то время, когда существовало Индо-греческое царство.
В отличие от счета в русском языке — один (1), два (2), три (3), арабские цифры имеют свое название:
Как написать римские цифры на клавиатуре
.Для написания римских цифр на клавиатуре можно использовать несколько способов. К самому простому и довольно популярному относится – смена раскладки.
ASCII-коды
Первым способом для написания римских букв на клавиатуре является использование ASCII-кодов. Это некие шифры, которые водятся благодаря комбинации Alt и последовательном наборе цифр на дополнительной клавиатуре (Num Lock). При этом Num Lock должен находиться в постоянно включенном режиме. Конечно использовать данную систему достаточно трудно и мучительно, но при этом комбинация из таких кодов помогает написать даже самые сложные комбинации из римских цифр. Единственное, что под рукой должна всегда находиться таблица с комбинациями или вы просто должны запомнить все эти комбинации.
Функция Word
Следующим способ, который можно использовать для написания римских цифр – это специальный код в Microsoft Word.Для этого необходимо:
- Зайти в Microsoft Word.
- Зажать комбинацию клавиш CTRL + f9, после чего появятся скобки, благодаря которым вы будете получать необходимые римские числа.
- В скобках необходимо прописать данный текст
- После чего нажимаем клавишу f9 и у вас появляется римское число.
Этот способ является самым удобным, но чаще всего его используют если у вас под рукой нет помощника по римским цифрам или отсутствует интернет. Данный способ написания римских цифр позволяет сделать это только в Microsoft Word или других офисных приложениях.Также написать римские цифры можно с помощью интернета. Для этого необходимо вписать в любом поисковике римские цифры и система поиска предложит варианты римских цифр, которые можно будет скопировать и вставить в документ или другую программу.
Английская раскладка
Для этого необходимо:
- — Нажать сочетание клавиш Shift + ALT или CTRL + Shift.
- Выбрать английскую раскладку.
- Использовать некоторые буквы, как римские цифры.
Предположим 1 – это будет альтернатива английской букве I. Так продолжать можно до бесконечности. В основном можно использовать большие буквы, которые помогут написать даже самые длинные цифры или даты. Данный способ является очень удобным и простым, ведь его можно использовать абсолютно в любом текстовом документе, в приложении и даже в любых программах и играх. Комбинируя различные буквы, вы можете получить все необходимые цифры, а при правильном составлении букв, можно написать даже уравнения.
Типографские варианты
Этот раздел посвящен историческому развитию различных типографских вариантов и форм индийских цифр, используемых сегодня.
Индийские варианты
Поскольку астрономические наблюдения проводились систематически и на высоком уровне в Индии несколько тысяч лет назад, требовалось большое количество — лакх и крор ( хинди : लाख , Lakh ; करोड़ , Карор ). Один лакх равен 100000, крор равен 100 лакхам, то есть 10000000. Эти числа остались на Индийском субконтиненте, хотя они были официально обменены на систему тысяч, и их все еще можно найти в обычном языке там сегодня.
Арабские варианты
В арабском письме орфография развивалась справа налево от первоначально вертикальных букв на папирусах сверху вниз (они были склеены из вертикальных полос), которые затем поворачивались на 90 градусов для чтения. Также были отмечены индийские цифры, которые поэтому были частично повернуты в шрифте по сравнению с индийским оригиналом, а затем были адаптированы к графическому стилю арабского письма. Структура арабских слов индийских цифр основана на наивысшем приоритете (то есть левой цифре), как и в западных языках. Например, слово «10 000» ( ashrat alāf ) составлено из слова ashara, обозначающего 10, и 1000alf, обозначающего 1000. Однако, как и в западных языках, существуют особые правила, например, для десятков — например, название 19 — tisʕata-ʕschar от tisʕa для 9 и aschara для 10, как в случае с девятнадцатью в немецком языке. Числа записываются в виде цифр слева направо (в отличие от букв, которые пишутся справа налево на арабском языке). Положение цифр такое же, как в десятичной системе счисления (т.е. цифры с наивысшим приоритетом слева).
До того, как арабы приняли индийскую систему позиционных значений, они использовали буквы своего алфавита для обозначения чисел, которым, как и во многих других системах письма, таких как древнегреческий, римский или еврейский, в дополнение к звуковому значению присваивались числовые значения ( см. арабский алфавит ). Эта возможность до сих пор используется в определенных ситуациях, сравнимых с использованием римских цифр в западных лингвистических областях.
В Магрибе , то есть в арабоязычных странах к западу от долины Нила , традиционно используются цифры, идентичные европейским, а не символы, представленные здесь как арабские.
Европейские варианты
Заглавные буквы
Фигуры старого стиля
В Европе существует две основных формы представления цифр: прописные цифры и старый стиль цифр .
Самый распространенный вариант — заглавные буквы: все цифры имеют одинаковую высоту, а именно высоту заглавных букв (заглавных букв). Чтобы обеспечить чистый набор таблиц, все числа в верхнем регистре обычно имеют одинаковую ширину, а именно ширину полуквадрата . Этот вариант также известен как номера таблиц . Пропорциональные цифры в верхнем регистре , где 1, в частности, уже, чем другие цифры, встречаются реже . Недостатком цифр в верхнем регистре является то, что они образуют оптическое инородное тело в прокручиваемом тексте, и что с некоторыми полуквадратными цифрами (такими как 1) расстояние между буквами также кажется слишком большим.
По этой причине хорошо разработанные шрифты имеют второй набор цифр, цифры старого стиля. Как и строчные буквы, они имеют восходящие и нисходящие элементы и , как правило, индивидуальный интервал, адаптированный к форме символов . Это означает, что они органично и правильно вписываются в текст с типографской точки зрения. Некоторые шрифты также предлагают старые рисунки той же ширины для набора текста.
Японские числа от 1 до 10
Счет и написание до 10 на японском следующий:
- Один – ичи (一). При быстром произношении последняя гласная опускается, слово звучит как «ич».
- Два – ни (二).
- Три – сан (三). Хотя это созвучно с горой, иероглифы разные.
- Четыре – ен (альтернативное чтение – ши) (四).
- Пять – го (五).
- Шесть – року (六). Для не японца произнести это слово правильно непросто, поскольку первый звук – нечто среднее между р и л. При произнесении необходимо задействовать только кончик языка.
- Семь – нана, редко шичи (七).
- Восемь – хачи (八). При проговаривании необходимо сделать краткую паузу между слогами
- Девять – ку (九). Частая ошибка изучающих японский – превращение гласной в ю. Это неверно: в конце должна быть отчетливая у.
- Десять – дзю (十). Первая буква одновременно похожа на дз, ж и дж.
При подсчете объектов используются не только числительные, но и суффиксы, обозначающие, что именно считается. Если подобрать подходящий суффикс не удается, можно воспользоваться упрощенным счетом:
- Один – хитоцу (一つ). Первый знак соответствует ичи из приведенной выше последовательности, второй взят из хираганы.
- Два – футацу (二つ). Система образования аналогична описанной выше.
- Три – мицу (三つ). При произнесении между слогами делается небольшая пауза, а звук «ц» несколько удлиняется так, словно бы это полуторная буква. Если записать слово азбукой, оно будет выглядеть так: みっつ. Небольшой символ в центре означает удвоение следующего звука.
- Четыре – йоцу (四つ). Между слогами делается небольшая пауза.
- Пять – ицуцу (五つ).
- Шесть – мутцу (六つ). После первого слога делается маленькая пауза.
- Семь – нанацу (七つ). Проговаривая, необходимо сделать паузу перед последним слогом.
- Восемь – яцу (八つ).
- Девять – коконоцу (九つ). В речи делаются две паузы: после «коко» и следующего слога.
- Десять – то (十). Из десятка это слово – единственное без заключительного символа хираганы つ.
Система основана на кунном чтении, то есть традиционных японских цифрах.
Чтобы образовать порядковое числительное, достаточно добавить к каждому из кунных чисел знак 目 (ме). Хитоцуме – первый, футацуме – второй.

Счет в японском языке
Часть 2. Преобразование буква — цифра.
ОДИН. Что такое «одИн»? Если изменить ударение, то получится «Один» — древнегерманский языческий бог. Самый главный из всех богов. Бог №1.
Также, если возьмём слово «единица», то убрав первую букву, получим «Денница» — одно из имён Дьявола. Но это, конечно, случайное совпадение.
Как бы то ни было, мы можем предположить, что единица изначально имела мистический, религиозный смысл. Поэтому её начертание старались сохранять. К тому же мы не должны забывать, что «римские цифры» появились раньше, чем современные «арабские». Следовательно, можно предположить, что современная цифра «1» произошла от «римской» цифры «I»:
Приведём несколько высказываний Блаватской из её «Тайной доктрины» в отношении скрытого смысла символа единицы:
ДВА. В своей статье Фоменко в качестве доказательства приводит фото фрагментов старых текстов:
Также он очень аргументировано и достаточно убедительно утверждает, что «в русском почерке конца XVIII века цифра «2» и буква «Д» писались одинаково. Вероятно потому, что «д» — это первая буква слова «два». Полное тождество буквы «д» и цифры «2» в почерке того времени очевидно, например, из надписи на другом рисунке XVIII века, который мы приводим…»
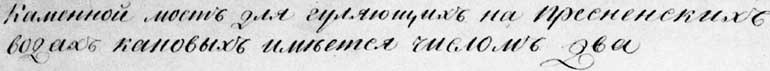 |
Предположим, что это действительно было так — букву Д и цифру 2 иногда или часто заменяли или путали. Заменять могли ради красоты почерка. Ведь, согласитесь, цифра «2» на приведённых фото выглядит очень эффектно. Но из этих рассуждений совершенно не ясно, что из чего произошло. Что первично и что вторично? Лично мне представляется более вероятным, что цифры произошли из букв, а не наоборот.
или
Если это так, тогда рассмотрим другие цифры.
ТРИ. Первую букву этого слова можно превратить в цифру, если положить её на бок. При этом не будем забывать про старое изображение этой буквы.
ЧЕТЫРЕ. Первая буква этого слова настолько сильно совпадает с цифрой «Ч», что нашим предкам пришлось создать вариант написания этой цифры в виде «4». Однако это сделано только в печатных изданиях. А от руки мы продолжаем писать четвёрку в виде буквы «Ч».
ПЯТЬ. Первую букву этого слова можно преобразовать в цифру «5» разными способами. Например, если взять две буквы «П» и соединить их валетом, то мы получим вполне современное изображение пятёрки:
хотя мне представляется более вероятным другой вариант её создания:
ШЕСТЬ. Опять смотрим на первую букву и делаем из неё цифру «6», положив букву «Ш» на бок. Нужно заметить, что это только один из вариантов.
СЕМЬ. Современная цифра «7» совершенно не похожа на первую букву — «С». Но, если мы посмотрим на рисунок, то станет понятно, что эта цифра раньше писалась иначе.
Давайте и мы опустим традиционную перемычку в самый низ.
Наша семёрка превратилась в букву Z.
Теперь, чтобы хоть немного оживить описание, приведу пример из художественного фильма «Азазель». Повествование этого фильма разделено на главы. Третья глава названа «Зутулый штудент».
 |
«Штудент» — потому что штудирует. А вот почему «зутулый», а не сутулый? Попробую предположить: раньше так говорили. Возможно, что так говорили не везде; возможно, что это был локальный говор. Но со временем звонкая «З» была заменена на глухую «С». Было «земь», стало «семь». Произношение изменилось, а цифра осталась прежней. Вот почему цифру «7» делали из буквы «Z». Это старое обозначение современной буквы «З».
Теперь нужно отметить, что процесс преобразования буквенных знаков в цифровые проходил не сразу. Вероятно, что у него даже не было единого плана. Поэтому, можно утверждать, что этот процесс до сих пор не закончен. Например, цифру «7» уже многие начинают писать без средней горизонтальной черты.
ВОСЕМЬ. Здесь совсем просто: первая буква этого слова — «В» — абсолютно похожа на цифру «8».
ДЕВЯТЬ. Здесь первая буква «Д». Но ведь эта буква уже была использована при создании двойки. К сожалению, это так. Но как же наши предки выкрутились? А вот как – из одной буквы «Д» были созданы две разные цифры «2» и «9».
или
Часть 3. Реконструкция событий.
Давным-давно наши предки решили основательно упорядочить свою жизнь. С этой целью они придумали календарь. По причине того, что периоды Луны были более короткими, а значит, легче заметными, чем солнечные. Поэтому, первым был создан лунный календарь, в котором 27 дней каждого месяца были разделёны на три периода (три недели) по 9 дней. В русских сказках эта информация сохранилась в виде слов: «у отца было три сына» (у месяца три периода), «тридевятое царство», «за тридевять земель». Да и умерших поминали на девятый день. Это очень удобно – не надо считать дни. Если в пятницу умер, то ровно через неделю, в следующую пятницу, поминают.
Действительно, славянская неделя состояла из девяти дней:
| 1. | ПонедЕльник. |
| 2. | ВтОрник. |
| 3. | ТретЕйник. |
| 4. | ЧетвЕрик. |
| 5. | ПятнИца. |
| 6. | ШестИца. |
| 7. | СедьмИца. |
| 8. | ОсьмИца. |
| 9. | НедЕля. |
Последний – девятый – день был выходным, когда ничего не делали. Потому он и назван «неделя». Здесь всё понятно. Но почему первый день недели назван не первиком или, к примеру, первейником? Ответ напрашивается сам собой: потому, что один или единица – это фаллический символ бога, его имя. А имя бога нельзя произносить в быту (в суе). Оно было тайным. Пришлось скрыть истинное название, и первый день назвали понедельником – тот, который после недели, после выходного дня.
Как мы видим, числа в те времена уже были или только начинали создаваться, но цифр ещё не было. Предполагается также, что письменность уже существовала. Естественно, что со временем встал вопрос обозначения чисел при письме.
Как бы то ни было, но именно эти девять дней, точнее – девять цифр, им соответствующих – легли в основу первой, древней системы счисления. Со временем, после изобретения ноля, эта система стала десятичной. И десять пальцев на руках не имеют к этой системе никакого отношения. Это просто совпадение.
Telecar.
24 июня 2014 г.
Особенности арабской цифры 0 (ноль)
Ноль понимается как отсутствие числового значения или разряда. Ноль — очень полезная цифра хотя бы тем, что позволяет производить вычисления в столбик. Ни в одной другой числовой системе нет возможности это сделать. Чтобы убедиться в этом, попробуйте сделать расчет в столбик, используя римские цифры. Ноль придумали тоже индийцы и названа была эта цифра «сунья». На индийском значит — «пустой». В древних арабских странах этот знак еще называли cifra.
Таблица с названиями
Российский математик и педагог Магницкий называет ноль также — цифра или ничто. Часто её название использовали для первой страницы книг. Есть и другие источники, в которых можно найти старое название 0 — цифра. Чаще всего оно встречается в рукописях русских и европейских ученых 17-18 века.
Латинские буквы
Для начала давайте вспомним как обозначаются римские цифры:

Формально, для обозначения используются латинские буквы, поэтому их можно использовать для обозначения римских цифр. Для этого я приведу несколько примеров, что бы вы поняли.
Возьмем цифру 1 — это латинская буква I (большая буква i на английской раскладке).
2,3 — II и III соответственно.
4 — сочетание букв IV. Вы же не забыли забыли, что в указанном случае из большей цифры вычитается меньшая?
5 — V.
6 — VI. В конкретном случае цифры складываются.
7,8 — VII и VIII соответственно.
9, 11 — IX и XI соответственно.
10 — X.
21 — XXI.
24, 26 — XXIV и XXVI.
34 — XXXIV.
51 — LI.
378 — CCCLXXVIII.
В общем, суть, думаю, вам ясна. Пользоваться римскими цифрами совсем несложно, если не забывать правила построения.