Формула для расчета аннуитетного платежа в excel

Популярные вопросы по калькулятору

Можно ли в калькуляторе менять ставку по кредиту?

Да, изменение ставки возможно. Для этого добавьте досрочное погашение с типом «Изменение ставки». Новая ставка будет действовать обычно с ближайшей даты очередного платежа

Можно ли внести ежемесячные досрочные погашения?

Да, такое возможно. Нужно добавить досрочное погашение с типом «Ежемесячное уменьшение срока» или суммы. Каждый месяц в дату, указанную при добавлении гашения будет добавляться досрочка на заданную сумму.

Возможен ли расчет досрочки с материнским капиталом?

Досрочное погашение материнским капиталом ничем не отличается от обычного досрочного погашения. Нужно указать дату внесения и сумму материнского капитала. В случае Сбербанка если капитал внесен не в дату очередного платежа, то часть капитала пойдет на погашение процентов.

Как рассчитать аннуитетный платеж в Excel

Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.

Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.

Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:

Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.

Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:

Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:

Здесь нам требуется заполнить три поля:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12.
• «Кпер» – общий срок кредитования.
• «Пс» – сумма кредита (указывается со знаком минус).

Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4). Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус

Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.

После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:

Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.

Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ». По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках

Можно было просто вписать в строке формул то, что там сейчас вписано

По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.

Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:

На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.

Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.

Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.

Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:

График выплат

Сохранить в pdf Сохранить в Excel Распечатать Cсылка на расчет

Дата платежа	Остаток задолженности, руб.	Начисленные %, руб.	Платеж в основной долг, руб.	Сумма платежа, руб.
08.10.2018	310 000,00	3 821,92	3 552,96	7 374,88
08.11.2018	306 447,04	3 904,05	3 470,83	7 374,88
08.12.2018	302 976,21	3 735,32	3 639,56	7 374,88
08.01.2019	299 336,66	3 813,47	3 561,41	7 374,88
08.02.2019	295 775,25	3 768,10	3 606,78	7 374,88
08.03.2019	292 168,46	3 361,94	4 012,94	7 374,88
08.04.2019	288 155,52	3 671,02	3 703,86	7 374,88
08.05.2019	284 451,67	3 506,94	3 867,94	7 374,88
08.06.2019	280 583,73	3 574,56	3 800,32	7 374,88
08.07.2019	276 783,41	3 412,40	3 962,48	7 374,88
08.08.2019	272 820,93	3 475,66	3 899,21	7 374,88
08.09.2019	268 921,71	3 425,99	3 948,89	7 374,88
08.10.2019	264 972,83	3 266,79	4 108,09	7 374,88
08.11.2019	260 864,74	3 323,35	4 051,53	7 374,88
08.12.2019	256 813,20	3 166,19	4 208,69	7 374,88
08.01.2020	252 604,51	3 218,11	4 156,77	7 374,88
08.02.2020	248 447,75	3 165,16	4 209,72	7 374,88
08.03.2020	244 238,03	2 910,78	4 464,10	7 374,88
08.04.2020	239 773,93	3 054,65	4 320,22	7 374,88
08.05.2020	235 453,71	2 902,85	4 472,02	7 374,88
08.06.2020	230 981,68	2 942,64	4 432,23	7 374,88
08.07.2020	226 549,45	2 793,08	4 581,80	7 374,88
08.08.2020	221 967,64	2 827,81	4 547,07	7 374,88
08.09.2020	217 420,57	2 769,88	4 605,00	7 374,88
08.10.2020	212 815,57	2 623,75	4 751,12	7 374,88
08.11.2020	208 064,45	2 650,68	4 724,19	7 374,88
08.12.2020	203 340,25	2 506,93	4 867,94	7 374,88
08.01.2021	198 472,31	2 528,48	4 846,40	7 374,88
08.02.2021	193 625,91	2 466,74	4 908,14	7 374,88
08.03.2021	188 717,78	2 171,55	5 203,33	7 374,88
08.04.2021	183 514,44	2 337,92	5 036,95	7 374,88
08.05.2021	178 477,49	2 200,41	5 174,47	7 374,88
08.06.2021	173 303,02	2 207,83	5 167,05	7 374,88
08.07.2021	168 135,97	2 072,91	5 301,97	7 374,88
08.08.2021	162 834,00	2 074,46	5 300,42	7 374,88
08.09.2021	157 533,59	2 006,93	5 367,94	7 374,88
08.10.2021	152 165,64	1 876,01	5 498,86	7 374,88
08.11.2021	146 666,78	1 868,49	5 506,38	7 374,88
08.12.2021	141 160,40	1 740,33	5 634,54	7 374,88
08.01.2022	135 525,85	1 726,56	5 648,32	7 374,88
08.02.2022	129 877,54	1 654,60	5 720,27	7 374,88
08.03.2022	124 157,26	1 428,66	5 946,22	7 374,88
08.04.2022	118 211,04	1 505,98	5 868,90	7 374,88
08.05.2022	112 342,14	1 385,04	5 989,84	7 374,88
08.06.2022	106 352,30	1 354,90	6 019,98	7 374,88
08.07.2022	100 332,32	1 236,97	6 137,90	7 374,88
08.08.2022	94 194,42	1 200,01	6 174,87	7 374,88
08.09.2022	88 019,55	1 121,34	6 253,53	7 374,88
08.10.2022	81 766,02	1 008,07	6 366,80	7 374,88
08.11.2022	75 399,21	960,57	6 414,31	7 374,88
08.12.2022	68 984,90	850,50	6 524,38	7 374,88
08.01.2023	62 460,52	795,73	6 579,15	7 374,88
08.02.2023	55 881,37	711,91	6 662,96	7 374,88
08.03.2023	49 218,41	566,35	6 808,53	7 374,88
08.04.2023	42 409,88	540,29	6 834,59	7 374,88
08.05.2023	35 575,29	438,60	6 936,28	7 374,88
08.06.2023	28 639,01	364,85	7 010,03	7 374,88
08.07.2023	21 628,99	266,66	7 108,22	7 374,88
08.08.2023	14 520,77	184,99	7 189,89	7 374,88
08.09.2023	7 330,88	93,39	7 330,88	7 424,27

Показать все

Как рассчитать размер аннуитетного платежа?

Существует специальная формула, которая позволяет рассчитать сумму, которую ежемесячно следует вносить для погашения долга перед банком и процентов по нему.

А = К х S

В этой формуле:

A – размер платежа

K – коэффициент аннуитета

S – сумма полученного кредита

Есть один неизвестный элемент формулы – коэффициент аннуитета. Его необходимо рассчитать отдельно по соответствующей формуле.

Здесь i – это месячная ставка процентов за пользование кредитом, которая рассчитывается путем деления годовой ставки на 12 месяцев

n – количество месяцев, на протяжении которого кредит необходимо погасить.

Эта формула поможет вам самостоятельно рассчитать сумму, которую следует вносить каждый месяц в пользу банка.

Платежи и проценты по кредиту

Тип платежа соискатель выбирает сам, исходя из периодичности и размера личных финансовых поступлений. Аннуитетные и дифференцированные выплаты имеют существенные отличия, которые определяют их достоинства и недостатки.

Аннуитетный

Клиент совершает фиксированные ежемесячные взносы, первая часть которых идёт на погашение процентов по договору, вторая – уменьшает тело кредита. Проценты начисляются на фактическую сумму долга, а она с каждым периодом уменьшается, в последующих выплатах соотношение частей будет изменяться. При этом сумма основного платежа останется неизменной.

Кредитный калькулятор при выборе аннуитета по заданным соискателем параметрам рассчитывает:

1. Процентную ставку за платёжный период, чаще всего это 1 месяц (ПСМ). Вычисляется следующим образом: ПСГ/100/12 (количество месяцев в году).

1. Коэффициент аннуитета (КА) по формуле, где * — степень, равная общему количеству платежей:

ПСМ x (1 + ПСМ) *

(1 + ПСМ) * — 1

1. Сумму аннуитетного платежа (АП), которая равна: ОД x КА.

1. Проценты (СП) по формуле, где СЗ – размер фактической задолженности, которая в первом взносе всегда равна ОД: СЗ x ПСМ.

1. Их долю (ДСП): АП – СП.

1. Долю погашения ОД (ДОД): АП – ДСП.

Анализ расчётов, диаграммы и графика онлайн-сервиса Сбербанка покажет, что аннуитетный тип наиболее выгоден для финансового учреждения (переплата выше, чем при дифференцированном). Но он удобен для клиентов, которые получают стабильный фиксированный доход.

 Дифференцированный

На практике данный тип платежей применяется для ипотечных кредитов, но нередко банки используют его для потребительских программ. Главное отличие – стабильное уменьшение суммы ежемесячного платежа на протяжении всего срока действия договора. Основная финансовая нагрузка приходится на первые месяцы. Доля погашения ОД остаётся фиксированной для каждого периода, а размер процентов уменьшается.

Алгоритм расчёта параметров кредита с дифференцированным типом выплат для онлайн-калькулятора выглядит проще и состоит из вычислений:

1. Доли платежей, ежемесячно погашающих ОД – соотношение ОД и количества периодов срока кредитования (количество месяцев).
2. Доли процентов: произведение фактического ОД на ПСМ.
3. Размер дифференцированного платежа (ДП) для каждого периода: сумма доли процентов и ОД.

Проценты так же начисляются на остаток ОД, то есть их сумма становится меньше с каждым периодом.

Анализ результатов кредитного калькулятора покажет, что при строгом соблюдении графика выплат, дифференцированный тип предпочтительнее для некоторых клиентов, так как уменьшает переплату по продукту.

С помощью формул, соискатель может провести все расчёты по кредиту самостоятельно, но проще доверить эту работу кредитному калькулятору.

Основная формула аннуитетного платежа в Excel

Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:  

Основные значения формулы расшифровываются так:

• АП – аннуитетный платеж (название сокращено).
• О – размер основного долга заемщика.
• ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
• С – число месяцев, на протяжении которых длится кредитование.

Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.

Примеры использования функции ПЛТ в Excel

Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:

1. Составить общую таблицу в Excel по исходным данным.

Таблица, составленная по условию задачи. В действительности можно задействовать другие столбцы для ее размещения

1. Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
2. В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
3. В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
4. Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».

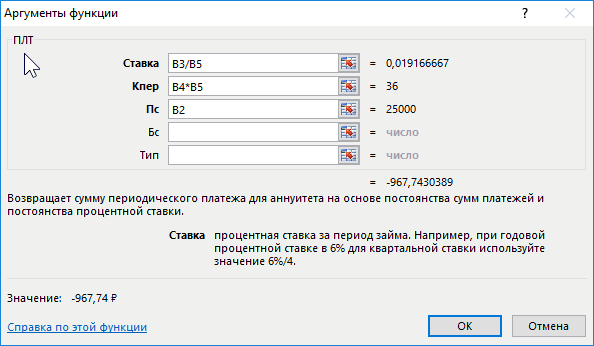Необходимые действия в окне «Аргументы функции». Здесь указан порядок заполнения каждого параметра

1. Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».

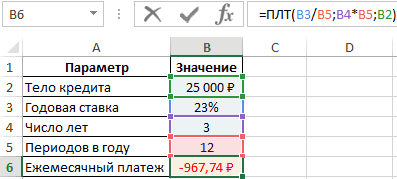Финальный результат. Ежемесячный платёж посчитан и выделен красным цветом

Пример расчета суммы переплаты по кредиту в Excel

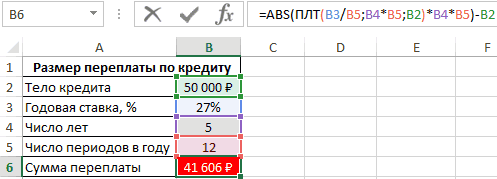
В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:

1. Составить исходную таблицу данных.

Таблица, составленная по условию задачи

1. Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
2. В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.

Финальный результат. Практически двукратная переплата

Формула вычисления оптимального ежемесячного платежа по кредиту в Excel

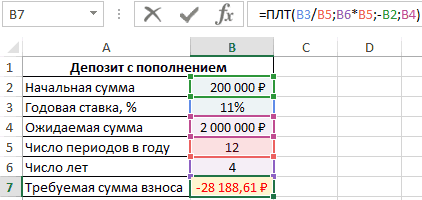
Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:

1. Составить табличку по исходным данным.

Таблица, составленная по данным из условия задачи

1. В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
2. Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.

Окончательный результат расчета

Особенности использования функции ПЛТ в Excel

В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; ; ). У функции есть следующие особенности:

Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.

Расчет в Excel суммы кредита для заданного аннуитетного платежа

В чём «фишка» аннуитетной схемы погашения кредита? Правильно! Основная «фишка» в том, что заёмщик выплачивает кредит равными суммами на протяжении всего срока кредитования. С такой схемой очень удобно планировать свой бюджет. Например, вы готовы ежемесячно выделять на погашение кредита 5000 рублей. По вашим скромным подсчётам, такая нагрузка будет для вас не слишком обременительной. Естественно, у вас возникает закономерный вопрос: «А на какую сумму кредита я могу рассчитывать?» В общем, нам нужен новый кредитный калькулятор, у которого в исходных данных будет не сумма кредита, а величина аннуитетного платежа.

Что же, друзья, не будем терять время! Открываем программу Microsoft Excel и приступаем к разработке нашего кредитного калькулятора!

Итак, структура нового кредитного калькулятора почти не изменилась. Здесь также есть блок с исходными данными и блок с расчётами. Единственное изменение, это то, что в исходных данных мы вводим ежемесячный аннуитетный платёж, который готовы выплачивать, а в расчётах получаем сумму кредита, на которую мы можем рассчитывать. Собственно, она на нашем рисунке обведена и отмечена под номером 1.

Чтобы рассчитать сумму ожидаемого кредита надо воспользоваться функцией ПС, предварительно кликнув по ячейке, в которой мы хотим видеть свой расчёт (в нашем калькуляторе это ячейка с координатой C11). Вызвать функцию ПС можно нажав на знакомую вам кнопку «fx», которая находится слева от строки формул. В появившемся окне выбираем «ПС» и жмём «Ок». В открывшейся таблице вводим следующие данные:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12 (в нашем случае: C5/12).
• «Кпер» – общий срок кредитования (в нашем калькуляторе, это ячейка с координатой C6).
• «Плт» – ежемесячный аннуитетный платёж, перед которым ставим знак минус (в нашем калькуляторе, это ячейка C4, перед данной координатой мы и ставим знак минус).

Жмём «Ок» и в ячейке С11 появилась сумма 53 422 руб. – именно на такой размер кредита может рассчитывать заёмщик, который готов на протяжении 12 месяцев ежемесячно выплачивать по 5000 руб.

Кстати, обратите внимание на данные в строке формул (на рисунке они обведены и указаны под номером 2). Вы всё правильно поняли, друзья! Да, это те данные, которые необходимы для расчёта суммы кредита в нашем калькуляторе: =ПС(C5/12;C6;-C4)

Те самые параметры, которые мы вводили в таблице функции ПС.

Расчёт остальных показателей выполняется по такому же принципу, как и в предыдущем калькуляторе:

• Общая сумма выплат – это ежемесячный аннуитетный платёж (ячейка С4) умноженный на общий срок кредитования (ячейка С6). В строку формул вводим следующие данные: =C4*C6.
• Переплата (проценты) по кредиту – это общая сумма выплат (ячейка С12) минус сумма кредита (ячейка С11). В строку формул записываем: =C12-C11.
• Эффективная процентная ставка (или полная стоимость кредита) – это общая сумма выплат (ячейка С12) делённая на сумму кредита (ячейка С11) и минус единица. Затем всё это делим на срок кредитования, выраженный в годах (ячейка C6 делённая на 12). В строку формул записываем: = (C12/C11-1)/(C6/12).

Кстати, интересный момент. Вот в нашем примере, выплачивая ежемесячно в течение года по 5000 рублей, мы можем рассчитывать на сумму кредита равную 53 422 рубля. А что делать, если надо больше денег? Как вариант, можно увеличить срок кредитования. Если вместо 12 месяцев поставить 24, то сумма кредита увеличится до 96 380 рублей. Эти данные нам мгновенно выдал наш кредитный калькулятор, который вы можете скачать ссылке ниже:

Скачать калькулятор расчёта суммы аннуитетного кредита в Excel

Как создать кредитный калькулятор в Excel?

Добрый день уважаемый пользователь!

Сегодня я хотел бы поговорить о таком необходимом зле, как кредит. Почему зло, вы и так знаете, особенно это касается потребительского кредитования, когда за вещь вы переплачиваете в 2-3 раза больше ее реальной цены. Это всё необходимо учитывать и просчитывать, поэтому и научитесь создавать свой личный кредитный калькулятор в котором вы реально увидите картинку «мышеловки», в которую попадают обычный обыватель. Хотя есть еще кредиты для бизнеса, но там немного другая история, их берут, чтобы зарабатывать деньги. Главная проблема кредита даже не в «космических» процентах, а в том, что вы получаете удовольствие сейчас, а расплата и проблемы вас ждут в будущем, а это убивает личную мотивацию практически в зародыше. Пропадает желание, что-то делать, развиваться, напрягаться, учиться, создавать источники дохода, когда можно «тупо» взять паспорт и за 15 минут в ближайшем банке вас быстренько возьмут в кабалу и грамотно навешают на вас кучу всего разного и лишнего, лишь бы было, типа страховку и прочее.

Поэтому я очень хочу, чтобы материал, который я дам в своей статье будет вам полезен в принятии ваших решений.

Несмотря на то, что я не являюсь приверженцем кредитов, всё же осознаю их необходимость. Недавно мой ребенок попал в больницу, и я был вынужден, в силу обстоятельств, использовать средства кредитной линии. Ну а потом на протяжении 2 недель полностью закрыл долг, не отлаживая его в долгий ящик. Ну не мог я по-иному, нужны были деньги и срочно, ну и долг я сразу же закрыл и не ждал ни окончания льготного периода, ни начисления процентов.

Вот исходя из этих соображений и всё же возникновению необходимости получения кредита вами или вашими близкими, необходимо, я бы сказал желательно, перед путешествием в банк прикинуть ориентировочно сумму, сроки переплаты и т.п. После того как вы прочувствуете цифры вы или будете готовы оформить кредит или попросту откажетесь от него. И в этом вопросе вам очень поможет Microsoft Excel.

Рассмотрим три самых популярных варианта использования кредитного калькулятора в Excel:

Формула для расчета процентной части

Большинству клиентов, оформляющих ссуду или кредит в банке, интересно знать эффективную процентную ставку. В этом параметре отражается общая переплата по всему кредиту, включающая все предусмотренные финансовой организацией комиссии и платежи.

Для примера возьмем расчет кредита в полмиллиона рублей на два года с процентной ставкой 12% и ежемесячной комиссией 1% (снимается ежемесячно со всей суммы) при аннуитетных платежах. Основная задолженность рассчитывается в разнице аннуитетных платежей и процентов. Сумма процентов будет произведением месячной ставки на остаток долга, который равен разнице от остатка предыдущего периода и суммы основного долга в прошлом периоде.

В итоге по расчетам нужно будет вернуть банкирам от полумиллиона 684881,67 руб. Соответственно разница – 184 881, 67 руб. Тогда эффективная процентная ставка окажется на уровне 37%. Если же вести расчет без учета однопроцентной комиссии, то выйдем на эффективную процентную ставку в 13%.

Популярные вопросы по вкладам

Как рассчитать проценты по вкладу в банке?

Для расчета нужно сумму вклада умножить на число дней, в течение которого был открыт вклад, умножить на ставку по депозиту, деленную на 100%. Полученную сумму нужно разделить на число дней в году(365 или 366). Проще воспользоваться универсальным калькулятором вкладов на нашем сайте.

Что такое процентная ставка по вкладу

Процентная ставка по вкладу — это число, которое определяет доходность вклада. Чем она выше, тем больше доходность. Различают простую и эффективную ставку по вкладу. Ставка по вкладам зависит от ключевой ставки ЦБ.

Что такое капитализация процентов по вкладу?

Капитализация процентов по вкладу — это плюсование процентов, которые начислены за каждый период, к сумме вклада. К примеру, вы положили вклад на 1000 р и получили через месяц доход 10 р, эти 10 рублей плюсуются к сумме вклада — 1000 + 10 = 1010.

На новую сумму вклада начисляются проценты. Значит в следующем месяце вы получите больше.

Что значит проценты не капитализируются?

Проценты не капитализируются — это значит проценты не прибавляются к сумме вклада каждый месяц. Обычно они выплачиваются на определенный счет в виде дохода. Их можно снимать и пользоваться этими деньгами. С одной строны это хорошо, сразу получаешь доход. С другой — плохо, т.к. доход по вкладу не растет

Кредитный калькулятор для расчёта простых кредитов

     Начнём с простого варианта, быстро прикинем, сколько нам нужно ежемесячно оплачивать по аннуитетному кредиту, это когда выплаты делают одинаковыми суммами, как в большинстве случаев. Это можно произвести одной функцией Excel и несколькими простыми формулами. Для получения результата в Excel существует функция ПЛТ в разделе «Финансовые». 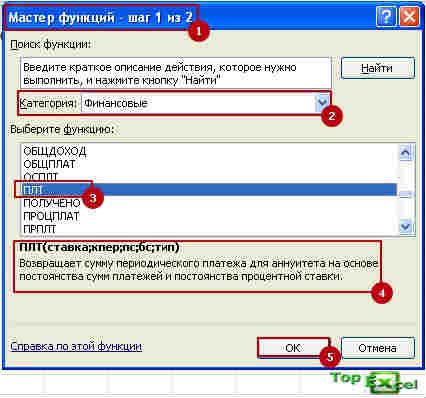     Указываем, в какую ячейку нужен результат, вызываем «Мастер функций» ищем функцию ПЛТ, нажимаем кнопочку «ОК» и в окне мастера вводим необходимые аргументы для нашего расчёта, формула получается следующего вида:

             =ПЛТ(B5/12;B6;B4;0;0), где:

• Ставка (B5/12) – является аргументом, указывающим на процентную ставку по взятому кредиту в разрезе периодов выплат, в нашем случае это месяцы. Если ставка по кредиту в год 18%, то за один месяц будет составлять 1,5%;
• Кпер (B6) – аргумент, указывающий на количество периодов, то есть, на сколько месяцев взят кредит;
• Бс (B4) – указываем, какую сумму кредита будем рассчитывать;
• Пс (0) – это финишная пряма, какой итог кредита должен быть в конце, скорее всего это будет 0, что означает, что вы никому и ничего не должны;
• Тип (0) – аргумент необходимый для учёта выплат каждый месяц. Если равно 1 – это учитываем выплаты к началу месяца, если 0 – то учитываем на конец. В постсоветском пространстве большинство банков используют последний вариант, а значит вводим 0.

      Кроме этого, необходимо рассчитать, сколько составит общая сумма выплаты, и какая переплата получится, когда вы вернёте деньги банку. Это легко осуществить при помощи простых формул. 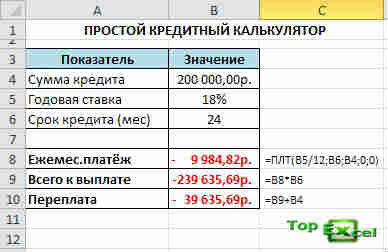     Теперь давайте немного улучшим и детализируем наш отчёт с помощью функции ОСПЛТ, которая определяет часть основного платежа по телу кредита и функции ПРПЛТ, которая посчитает всё, что касается процентов банку за использование кредита. Видоизменим ваш расчёт следующей таблицей: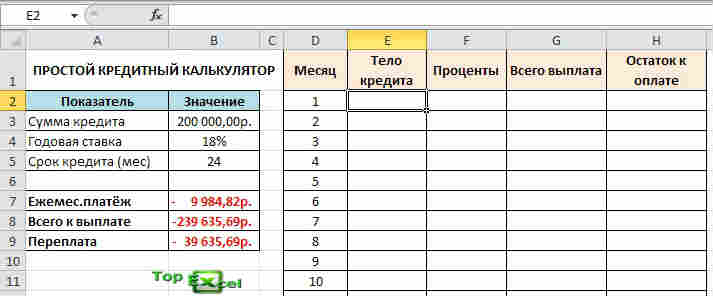

     Теперь в поле «Тело кредита» в ячейку Е2 вводим формулу функции ОСПЛТ следующего вида:

            =ОСПЛТ($B$4/12;D2;$B$5;$B$3;0)

   Как видите, ее орфография практически аналогична функции ПЛТ, добавился только аргумент «Период», который указывает на номер текущего месяца, и дополнительно рассматривать ее я не буду

Единственное, на что обращу ваше внимание, это то, что формула будет растянута на диапазон, а значит, аргументы необходимо закрепить абсолютными ссылками.      Следующим шагом для столбика «Проценты» будем использовать возможности функции ПРПЛТ

Вводится она аналогично вышеописанной и с теми же условиями и будет иметь такой вид:

             =ПРПЛТ($B$4/12;D2;$B$5;$B$3;0)      Теперь в оставшиеся столбики будем вводить простые формулы, для получения суммы выплаты нам нужна формула: =E2+F2, а для определения суммы остатка кредита используем формулу: =$B$3+СУММ($E$2:E2). 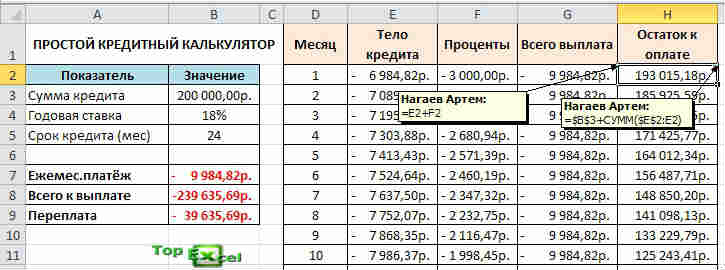    При необходимости, возможно, немножко улучшить и автоматизировать ваш кредитный калькулятор в Excel для уменьшения количества ошибок.

      Для начала пропишем формулу в ячейку D3 для того чтобы она подстраивала и отслеживала срок кредита:

          =ЕСЛИ(D2>=$B$5;»«;D2+1)

     Следующим шагом с помощью логической функции ЕСЛИ для поля «Тело кредита», сделаем автоматическую проверку достигли ли вы последнего срока выплат или нет. Если период, достигнут, получаем пустую ячейку «», а если нет, то функцией ОСПЛТ выводим необходимый расчёт:

         =ЕСЛИ(D3<>»»;ОСПЛТ($B$4/12;D3;$B$5;$B$3;0);»»)

Расчет суммы ежемесячных выплат

Произвести расчет суммы ежемесячных выплат в Excel можно, используя всего одну функцию.

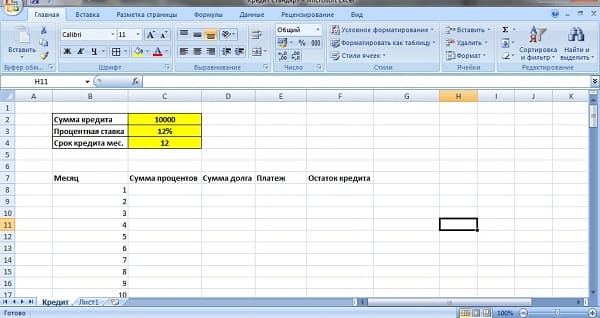
1. Откройте программу Microsoft Excel и введите в столбик А описание исходных данных: сумма кредита, годовая ставка, срок кредита (в месяцах), а также строку результата – сумма ежемесячных выплат. В столбик В мы будем заносить соответствующие значения.
2. Ставим курсор на ячейку результата (в нашем примере это ячейка В5) и в меню «Вставка» находим пункт «функция». Откроется окно Мастера функций
3. Выберите категорию «финансовые» и в окне функций выделите функцию ПЛТ
4. Далее необходимо указать ячейки, которые будут служить аргументами функции. Первый аргумент Ставка. Чтобы не вводить название ячейки вручную, окно мастера можно свернуть кнопкой в конце строки.
5. Сверните окно и выделите ячейку, в которой будете указывать ставку (в нашем примере это ячейка В2).
6. Нажмите на кнопку в конце строки аргумента, чтобы вернуться в окно мастера.
7. Так как ставку вы буде указывать годовую, а результат выплат нужно получить помесячный, то в строке аргумента заданное значение нужно разделить на 12. Дополните строку аргумента «/12»
8. Следующий аргумент – количество периодов. Таким же образом сверните окно и укажите ячейку значения «срок кредита» (у нас это ячейка В3)
9. Аргумент ПС означает сумму кредита, сверните окно мастера и укажите соответствующую ячейку (в нашем примере В1)
10. Аргумент БС выражает конечный баланс. Очевидно, что наша задача погасить кредит полностью, поэтому введите в строку значение аргумента «0». Аргумент Тип указывает на способ учета зачисления выплат – в начале периода (месяца) или в конце. Большинство кредитов выдается по второму типу учета, поэтому определите значение аргумента равным «0»
11. Нажмите кнопку ОК и формула готова. Введите исходные значения, и в результативной ячейке вы найдете сумму ежемесячных выплат. Она будет со знаком минус. Это означает, что деньги вам нужно отдавать…