Как высчитать процент из суммы (числа)?

Способ четвёртый: составляем пропорцию

Посчитать процент от суммы можно с помощью составления пропорции. Это ещё одно страшное слово из школьного курса математики. Пропорция – равенство между двумя отношениями четырёх величин. Для наглядности лучше сразу разобраться на конкретном примере. Вы хотите купить сапоги за 8 000 рублей. На ценнике указано, что они продаются со скидкой 25%. Сколько же это в рублях? Из 4 величин мы знаем 3. Есть сумма 8 000, которая приравнивается к 100%, и 25%, которые требуется посчитать. В математике обычно неизвестную величину называют X. Получается пропорция:

8000 – 100%

X –  25%

Для удобства подсчётов переводим проценты в десятичные дроби. Получаем:

8 000 – 1

X – 0,25

Решается пропорция так: Х = 8 000 * 0,25 : 1X = 2 000

2 000 рублей – скидка на сапоги. Вычитаем эту сумму из старой цены. 8 000 – 2 000= 6 000 рублей (новая цена со скидкой). Вот такая приятная пропорция.

Этим методом можно воспользоваться и для определения значения 100%, если знаете числовой показатель – допустим, 70%. На общекорпоративном собрании шеф объявил, что за год было продано 46 900 единиц товара, при этом план выполнен лишь на 70%. Сколько же необходимо было продать, чтобы выполнить план полностью? Составляем пропорцию:

100% – Х

70%  – 46 900

Переводим проценты в десятичные дроби, получается:

1 – Х

0,7 – 46 900

Решаем пропорцию: Х = 46 900 * 1 : 0,7Х = 67 000. Вот таких результатов работы ожидало начальство.

Как вы уже догадались, методом пропорции можно вычислить, сколько процентов составляет числовой показатель от суммы. Например, выполняя тест, вы ответили правильно на 132 вопроса из 150. Сколько процентов задания было сделано?

150 – 100%

132 – Х%

Переводить в десятичные дроби эту пропорцию не надо, можно сразу решать.

Х = 100 * 132 : 150. В итоге Х = 88%

Как видите, не так уж всё и страшно. Немного терпения и внимания, и вот уже вычисление процентов вами осилено.

Факторы, развивающие интерес к учебе

Заметно, что если уделить немного времени решению процентных задач, то у любого проснется интерес, и математика станет неотъемлемой частью жизни. Но начинать учиться необходимо еще с детского сада. А еще лучше с самого рождения. Ребенок легче воспринимает науку в эти годы. Бытует мнение, что если упустить обучение до трех лет, то позже будет труднее привить ребенку любовь к школе, урокам

Существуют факторы, которые формируют заинтересованность человека к математике: доброе отношение учителя, внимание родителей, похвала и правильная активная методика обучения (попытаться увлечь ребенка и превратить задачу в захватывающее приключение). Ведь даже самая сложная задача может стать увлекательной

Учитель должен быть в первую очередь психологом и находить подход к каждому ученику, готовить индивидуальные занятия. Это сможет развить уверенность и чувство собственного достоинства в детях.

Добросовестный учитель разрабатывает разные соревнования, сценки, математический КВН для того, чтобы дети полюбили его науку и другие предметы в школе и дошкольном учреждении. Это разжигает энтузиазм в детях. Обучение через сказку понравится всем. Некоторые преподаватели дают задания домой, к примеру, написать сказочное сочинение на тему «Путешествие в страну математики». И дети включают свое воображение и пишут увлекательные истории. В этом случае ребята действительно полюбят школу! И тогда, повзрослев, дети найдут применение математике в любой области жизни. Да, всему человечеству стоит расширять свои познания в сфере процентных вычислений, несмотря на то что эта тема – одна из сложнейших. В каких классах изучаются задачи на проценты? Подробно эту тему разбирают только в пятых, шестых классах. Позже этому посвящается незначительная часть времени. Поэтому каждому, кто сталкивается с процентными вычислениями, придется вспомнить математику средних классов. Как оказалось, это сделать несложно. Кто придумал это?

Делим на 100

Если разделить число на сто, вы получите числовой эквивалент равный 1%. Чтобы дальше найти процент от суммы, умножьте на 1%, а чтобы перевести число в проценты, разделите на 1%.

Например, вы хотите купить чай по акции. Его обычная цена 150 рублей, а сейчас на него действует скидка 7%. Однако, у вас также есть карта данного магазина, и по ней чай будет стоить 132 рубля. Какой из вариантов выгоднее?

Переведите 7% в рубли. Для этого разделите сначала 150 на 100. Получается, 1% равен 1,5 рубля. Теперь умножаем 1,5 на 7, выходит 10,5 рублей. Вычитаем из полной стоимости чая полученную скидку в рублях. Выходит, что цена чая со скидкой – 139,5 рубля. Значит, выгоднее купить товар по карте.

Другой пример. Вы зашли на сайт и видите, что вещь, которая вам давно приглянулась стоит 2000 вместо 3000. Посчитаем, сколько составила скидка. Итак, делим 3000 на 100 и получаем 30. Это 1% старой цены. Теперь новую цену, то есть 2000 делим 1%. 2000/30 = 66,6666%

100 – 66,6666 = 33,3333% — размер скидки, которую предоставил магазин.

Способ второй: переводим проценты в десятичную дробь

Как вы помните, процент — сотая часть числа. В виде десятичной дроби это 0,01 (ноль целых одна сотовая). Следовательно, 17% – это 0,17 (ноль целых, семнадцать сотых), 45% – 0,45 (ноль целых, сорок пять сотых) и т. д. Полученную десятичную дробь умножаем на сумму, процент от которой считаем. И находим искомый ответ.

Например, давайте рассчитаем сумму подоходного налога от зарплаты 35 000 рублей. Налог составляет 13%. В виде десятичной дроби это будет 0,13 (ноль целых, тринадцать сотых). Умножим сумму 35 000 на 0,13. Получится 4 550. Значит, после вычета подоходного налога вам будет перечислена зарплата 35 000 – 4 550 = 30 050. Иногда эту сумму уже без налога называют «зарплатой на руки» или «чистой». В противовес этому сумму вместе с налогом «грязной зарплатой». Именно «грязную зарплату» указывают в объявлениях о вакансиях компании и в трудовом договоре. На руки же даётся меньше. Сколько? Теперь вы легко посчитаете.

Подсчет процента, разделив число на 10

Данный способ схож с прошлым, однако он проще и быстрее, если нужно рассчитать проценты кратные пяти.

Для этого вам нужно найти 10%, а затем делите или умножаете до тех пор, пока не найдете нужный для себя.

Предположим, вы положили 90 тысяч рублей в банк на год под удивительные 10% годовых, но без капитализации вклада. Долго ждать не хочется, интересно сразу понять, какая будет прибыль 12 месяцев. Для начала узнаем 10%. Делим 90 тысяч, передвигая запятую на один знак влево, получаем 9 тысяч. Будь речь о 5%, то 9 тысяч следовало бы разделить на 2, для расчета 40% – умножить на 4 и так далее. Этот способ очень удобен для работы с большими числами.

Виды процентных ставок по вкладам в банках

Открывая депозит в банке, у вас есть возможность решить, что вы хотите делать с начисляемыми дивидендами – выводить их на карту или прибавлять к сумме первоначального вклада, тем самым капитализируя его. В зависимости от того, какой вариант вы выберете, такой будет и формула расчета процентов. Если вы хорошо помните школьную математику, то вы знаете, что проценты бывают простыми, а бывают сложными.

Как начисляются простые проценты?

Итак, простая ставка по депозитам рассчитывается следующим образом:

Для удобства понимания давайте разберем такой пример: вы открываете в банке депозит на сумму в 50 000 рублей на 1 год с простым начислением процентов. Ставка % составляет 11,5%. Пользуясь вышеуказанной формулой, получается, что через год, после того как будет закрыт ваш депозит, вы заработаете:

В данном случае проценты не будут прибавляться к телу депозита, а каждый месяц (раз в полгода или раз в год) будут выводиться на другой ваш счет. Очень выгодно в таком случае пользоваться ежемесячным выводом процентов на дебетовые карты с начислением процентов на остаток. Если вы не успеваете потратить заработанные на депозите средства, на них будет начислен % по вашей карте.

Как начисляются сложные проценты?

Расчет сложных процентов по вкладу несколько сложнее и интереснее. Однако, прежде, чем мы приступим к его изучению, я предлагаю вам выяснить, в каких случаях мы имеем дело со сложной ставкой.

Открывая в банке депозит, вы вправе решать, прибавлять к нему полученные проценты или выводить их на другой счет. В случае, если вы выбираете первый вариант, по вашему вкладу начисляется сложный процент. То есть, в каждом последующем периоде % начисляются на большую сумму, нежели в предыдущем, тем самым ускоряя рост размера депозита.

Это присоединение выплат по депозиту к первоначальной сумме вклада очень важно, поскольку сумма накоплений растет все быстрее и быстрее. Причем, моделью роста выступает не арифметическая прогрессия, а экспонента

Для сравнения давайте возьмем расчет простых и сложных процентов по одному и тому же вкладу. Условно положим на счёт 100 000 рублей под 10% годовых. В конце расчетного периода по простой ставке мы получим:

100 000 * 10 / 100 = 10 000 рублей;

Чтобы посчитать доходность вкладов с капитализацией выведем общую формулу:

Формула сложных процентов представлена ниже:

Переменные означают следующее,

Рассчитываем наш пример:

100 000 * (1+0,833*365 / 100*365)^12 = 10 466,92 рублей

Таким образом, один и тот же депозит, положенный в банк на разных условиях, может принести как 10 000 рублей чистой прибыли, так и 10 466 рублей.

В последнем случае мы имеем дело с капитализацией депозита – добавлением начисленных % к телу депозита. Как результат, получаем рост первоначальной суммы инвестиции и начисление % на увеличенную сумму.

Чтобы не считать доходность депозита вручную, советую вам воспользоваться калькулятором сложных процентов. В нем вы сможете указать суммы регулярных довложений за определенный период. Найти такой калькулятор можно на моем сайте с правой стороны, в сайдбаре, во вкладке «Калькулятор доходности».

Как начисляется эффективная ставка?

Ну а теперь давайте разберемся с эффективной процентной ставкой по депозиту, чтобы собрать в голове полную картинку банковских предложений.

Эффективной ставкой принято называть ставку, дающую равнозначный доход по идентичному депозиту без капитализации процентов. То есть, предположим, что вы открываете счёт в размере 50 000 на год под 8% годовых с условием капитализации. Проводим расчет по уже известной нам формуле и получаем:

50 000 * (1+0,6666*365/100*365) 12 = 54 150 рублей.

А теперь смотрим на предложение в соседнем банке. Здесь вы можете открыть тот же самый депозит, но без капитализации, зато под 8,3% годовых. Такое предложение позволит вам получить точно такой же доход, как в случае с капитализацией.

(50 000 * 8,3 * 365/365) / 100 = 4 150 рублей.

Чтобы быстро рассчитать эффективную ставку по депозиту, достаточно сделать следующее:

Именно эти 8,3% и являются нашей эффективной годовой ставкой по депозиту с ежемесячной капитализацией. То есть, если вклад без прибавления процентов к телу депозита будет иметь ставку, превышающую 8,3%, то такое вложение будет для нас более выгодно, нежели депозит с 8% годовых и ежемесячной капитализацией. Не забываем, что в случае с вкладом с 8.3% годовых, ежемесячный процент можно перевести на дебетовую карту с начислением на остаток, в этом случае этот вклад будет выгоднее.

Что такое процент?

В повседневной жизни дроби   встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.

Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.

Дробь    означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.

Процентом является одна сотая часть

Например,  от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.

от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.

Еще пример,   от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.

Проценты встречались настолько часто, что люди заменили дробь  на специальный значок, который выглядит следующим образом:

Эта запись читается как «один процент». Она заменяет собой дробь  . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь    в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:

1% =  = 0,01

Два процента в дробном виде будут записаны как  , в виде десятичной дроби как 0,02 а с помощью специального значка два процента записывается как 2%.

2% =  = 0,02

Расчет процентов в Excel

Эксель умеет выполнять многие математические задачи, в том числе и простейший расчет процентов. Пользователю в зависимости от потребностей не составит труда рассчитать процент от числа и число по проценту, в том числе и в табличных вариантах данных. Для этого следует лишь воспользоваться определенными формулами.

Вариант 1: Расчет процентов от числа

Прежде всего давайте выясним, как рассчитать величину доли в процентах одного числа от другого.

Формула вычисления выглядит следующим образом: .
Чтобы продемонстрировать вычисления на практике, узнаем, сколько процентов составляет число 9 от 17

Выделяем ячейку, куда будет выводиться результат и обязательно обращаем внимание, какой формат указан на вкладке «Главная» в группе инструментов «Число». Если формат отличен от процентного, обязательно устанавливаем в поле параметр «Процентный».
После этого записываем следующее выражение: .

Впрочем, так как мы задали процентный формат ячейки, дописывать значение «*100%» не обязательно. Достаточно ограничиться записью «=9/17».

Чтобы посмотреть результат, жмем на клавишу Enter. В итоге получаем 52,94%.

Теперь взглянем, как можно вычислять проценты, работая с табличными данными в ячейках.

1. Допустим, нам требуется посчитать, сколько процентов составляет доля реализации конкретного вида товара от общей суммы, указанной в отдельной ячейке. Для этого в строке с наименованием товара кликаем по пустой ячейке и устанавливаем в ней процентный формат. Ставим знак «=». Далее щелкаем по клеточке с указанием величины реализации конкретного вида товара «/». Потом — по ячейке с общей суммой реализации по всем товарам. Таким образом, в ячейке для вывода результата у нас записана формула.

Чтобы посмотреть значение вычислений, нажимаем Enter.

Мы выяснили определение доли в процентах только для одной строки. Неужели для каждой следующей строки нужно будет вводить подобные вычисления? Совсем не обязательно. Нам надо скопировать данную формулу в другие ячейки. Однако поскольку при этом ссылка на ячейку с общей суммой должна быть постоянной, чтобы не происходило смещение, то в формуле перед координатами ее строки и столбца ставим знак «$». После этого ссылка из относительной превращается в абсолютную.

Наводим курсор в нижний правый угол ячейки, значение которой уже рассчитано, и, зажав кнопку мыши, тянем ее вниз до ячейки, где располагается общая сумма включительно. Как видим, формула копируется и на все другие клетки таблицы. Сразу виден результат подсчетов.

Можно посчитать процентную долю отдельных составляющих таблицы, даже если итоговая сумма не выведена в отдельную ячейку. После форматирования ячейки для вывода результата в процентный формат ставим в ней знак «=». Далее кликаем по ячейке, чью долю надо узнать, ставим знак «/» и набираем сумму, от которой рассчитывается процент. Превращать ссылку в абсолютную в этом случае не нужно.

Затем жмем Enter и путем перетягивания копируем формулу в ячейки, которые расположены ниже.

Вариант 2: Расчет числа по проценту

Теперь посмотрим, как рассчитать число от общей суммы по проценту от нее.

1. Формула для расчета будет иметь следующий вид: . Следовательно, если нам понадобилось посчитать, какое число составляет, например, 7% от 70, то просто вводим в ячейку выражение «=7%*70». Так как в итоге мы получаем число, а не процент, то в этом случае устанавливать процентный формат не надо. Он должен быть или общий, или числовой.

Для просмотра результата нажмите Enter.

Эту модель довольно удобно применять и для работы с таблицами. Например, нам нужно от выручки каждого наименования товара подсчитать сумму величины НДС, которая составляет 18%. Для этого выбираем пустую ячейку в строке с наименованием товара. Она станет одним из составных элементов столбца, в котором будут указаны суммы НДС. Форматируем ее в процентный формат и ставим в ней знак «=». Набираем на клавиатуре число 18% и знак «*». Далее кликаем по ячейке, в которой находится сумма выручки от продажи данного наименования товара. Формула готова. Менять формат ячейки на процентный или делать ссылки абсолютными не следует.

Для просмотра результата вычисления жмем Enter.

Копируем формулу в другие ячейки перетаскиванием вниз. Таблица с данными о сумме НДС готова.

Как видим, программа предоставляет возможность удобно работать с процентными величинами. Пользователь может вычислить как долю от определенного числа в процентах, так и число от общей суммы по проценту. Excel можно использовать для работы с процентами как обычный калькулятор, но также с его помощью легко и автоматизировать работу по вычислению процентов в таблицах.

Опишите, что у вас не получилось.
Наши специалисты постараются ответить максимально быстро.

Что такое проценты?

Это слово произошло от английского словосочетания Pro Centum

Прочитав это словосочетание, вы наверняка обратили внимание, что там присутствует слово цент. От этого и происходит смысл процентов

Как известно, цент — одна сотая часть от доллара. Поэтому 1% — это и есть одна сотая часть от числа.

Сейчас в процентах измеряются многие финансовые показатели:

1. налоги,
2. доли в бизнесе,
3. доходность от инвестиций,
4. премии и штрафы,
5. инфляция.

И не только финансовые:

1. рождаемость и смертность,
2. статистика удачных и неудачных браков,
3. коэффициент полезного действия.

Давайте разберёмся более подробно, как посчитать процент от суммы. Мы приведём вам несколько примеров, которые помогут вам все понять.

Пример 1. Водитель таксомоторной службы отработал смену. За день его выручка составила 5 тыс. рублей. Ему необходимо отдать службе такси комиссию с этих заказов — 15%. Чтобы узнать сумму, которую должен заплатить водитель, необходимо 5 тыс. умножить на 15, после чего разделить на 100. Мы получаем результат, равный 750 рублей. Как вы уже догадались, 15% — это 15 частей из ста.

Теперь мы приведём вам обратный пример с тем же водителем такси. Так, за смену он заработал 5 тыс. рублей. Он потратил определённую часть этих денег на обязательные расходы:

1. комиссию службе такси — 750 рублей,
2. мойку автомобиля — 250 рублей,
3. топливо — 1 тыс. рублей.

Итого у водителя остаётся 3 тыс. рублей. Из заработанных 5 тыс. рублей себе он забирает только 3. Теперь наша задача посчитать, какую часть от общей выручки он может смело положить к себе в карман. Для этого нам нужно разделить 3 тыс. на 5 тыс. После чего полученный результат, равный 0,6, умножить на 100%. Получается, водитель забирает себе в карман 60% от общей выручки.

Это интересно: разрядные слагаемые что это?

Пример 2. Четыре акционера открыли бизнес. Спустя год упорной работы он начал приносить доходы. Партнёры решили делить прибыль поровну, то есть каждому достанется по 25% от прибыли. Нам нужно посчитать, сколько денег получит каждый из них.

Допустим, бизнес приносит доход 200 тысяч рублей в месяц. Чтобы посчитать прибыль каждого из акционеров, необходимо умножить 200 тыс. на 25, и разделить на 100. Получаем результат — 50 тыс. рублей.

Пример 3. Конверсия продаж. Менеджер по продажам предлагает услуги своей компании по телефону. За месяц он совершил 800 звонков. Заинтересовались в услугах компании 280 клиентов. Для подсчёта конверсии продаж необходимо 280 разделить на 800, после чего умножить на 100. Результат будет равен 35%.

Формула для расчёта процента в соотношении двух чисел

Как известно, существует несколько вариантов формул для определения разницы в процентах между двумя числами. Применение простых формул натыкается на некоторые трудности при работе с отрицательными числами, а сложные формулы могут быть довольно громоздкими для использования.

Тем не менее обычно для вычисления разницы в процентах между числами используется следующая формула:

Где R — результат, Х – старый показатель, Y – новый.

Кроме этой простой формулы можно использовать более сложную:

Если х>у, тогда разница R может рассчитываться по формуле:

Если х<y, тогда разница может рассчитываться по формуле:

Также может применяться следующая формула:

Здесь а – первое число, b – второе.

В случае работы с отрицательными числами такая формула может выглядеть следующим образом:

Где а – первое число, b – второе число. Если же b>a, тогда необходимо поменять числа местами.

Как считать проценты в excel?

Если у вас под рукой имеется компьютер или ноутбук с операционной системой Windows, вам не составит большого труда подсчитать процент от необходимой суммы. Приведем для этого простой пример.

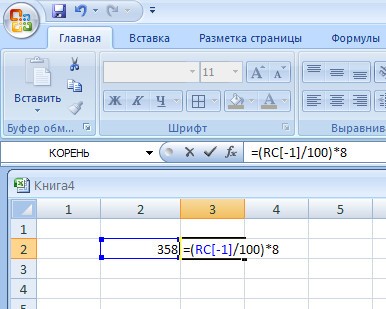
Нам необходимо найти 8% от 358.

1. Открываем Excel.
2. Находим свободную строку.
3. Вводим данные.
4. Ставим знак «=» и делаем подсчет.
5. Получаем 28,64.

Аналогично к подсчетам на калькуляторе, вы можете ввести в Excel знак %, и это тоже будет правильно.

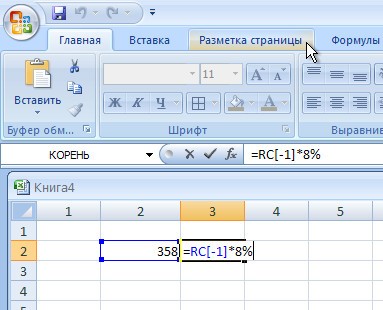
Иногда нам необходимо узнать процентный показатель от суммы.

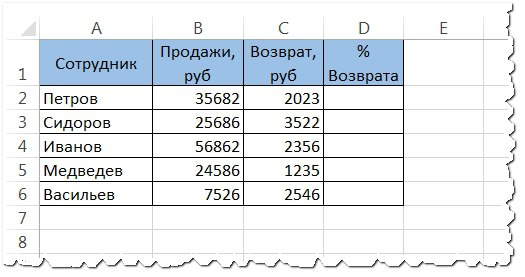
1. К примеру, у нас есть список сотрудников и сумма, на которую они произвели продаж. Помимо этого, известна сумма возвратов. По этим данным мы рассчитываем процент возвратов по товарам.
2. Просчитаем процент для первого показателя в списке — процент возвратов некоего Петрова.
3. Для начала составляем пропорцию, где 100% — это 35682(сумма продаж Петрова). х% — 2023 (сумма возвратов Петрова).
4. Решаем эту пропорцию по формуле, известной нам со школы.
5. Прописываем формулу в ячейке D2 и спускаемся немного вниз =C2*100%/B2.
6. К ячейке, в которой высветился результат, применяем формат «Процентный». Выделяем ячейки, правой кнопкой жмем на любой из них и выбираем «Формат». Во вкладке «Число» выбираем «Процентный». Система автоматически пропишет значок %.

7. Применив нашу формулу ко всем данным, получаем результат.

История возникновения процентных задач

Латинское выражение pro centum определяется как «за сотню», «со ста». Но произошло оно от итальянского слова, которое пишется как «сто». Однако еще существует предположение, что знак «%» (процент) появился через оплошность писателя книги. Он вместо «сто» напечатал %. Один инженер из Нидерландов как первооткрыватель выпустил в мир процентную таблицу расчетов в 1584 г. Сначала эта наука применялась в торговых областях, затем постепенно проценты стали использовать в технических работах, науке, хозяйственных делах, статистике. Можно сделать вывод, что математика и использование процентных вычислений очень пригодятся в жизни.

Задачи на проценты с решением

Как мы уже убедились, решать задачи на проценты совсем несложно. Для закрепления материала рассмотрим реальные примеры на проценты из учебников и несколько заданий для подготовки к ЕГЭ.

Задача 1. Организм взрослого человека на 70% состоит из воды. Какова масса воды в теле человека, который весит 76 кг?

Как решаем:

76 : 100 = 0,76 — 1% от массы человека

0,76 * 70 = 53,2

Ответ: масса воды 53,2 кг

Задача 2. Цена товара понизилась на 40%, затем еще на 25%. На сколько процентов понизилась цена товара по сравнению с первоначальной ценой?

Как решаем:

Обозначим первоначальную цену товара через х. После первого понижения цена станет равной.

х — 0,4х = 0,6x

Второе понижение цены составляет 25% от новой цены 0,6х, поэтому после второго понижения получим:

0,6х — 0,25 * 0,6x = 0,45x

После двух понижений изменение цены составит:

х — 0,45x = 0,55х

Так как величина 0,55x составляет 55% от величины x, то цена товара понизилась на 55%.

Ответ: 55%.

Задача 3. Четыре пары брюк дешевле одного пальто на 8%. На сколько процентов пять пар брюк стоят дороже, чем одно пальто?

Как решаем:

По условиям задачи стоимость четырех пар брюк — это 92% от стоимости пальто

100 — 8 = 92

Получается, что стоимость одной пары брюк — это 23% стоимости пальто.

92 : 4 = 23

Теперь умножим стоимость одной пары брюк на пять и узнаем, что пять пар брюк обойдутся в 115% стоимости пальто.

23 * 5 = 115

Ответ: пять пар брюк на 15% дороже, чем одно пальто.

Задача 4. Семья состоит из трех человек: муж, жена и дочь-студентка. Если зарплата мужа вырастет в два раза, общий доход семьи возрастет на 67%. Если дочери в три раза урежут стипендию, общий доход этой семьи уменьшится на 4%. Вычислить, какой процент в общий доход семьи приносит заработок жены.

Как решаем:

По условиям задачи общий доход семьи напрямую зависит от доходов мужа. Благодаря увеличению зарплаты общий доход семьи вырастет на 67%. Значит, зарплата мужа составляет как раз 67% от общего дохода.

Если стипендия дочери уменьшится в три раза (т.е. на 1/3), останется 2/3 — это и есть 4%, на которые уменьшился бы семейных доход.

Можно составить простую пропорцию и выяснить, что раз 2/3 стипендии — это 4% дохода, то вся стипендия — это 6%.

А теперь отнимем от всего дохода вклад мужа и дочери и узнаем, какой процент составляет заработок жены в общем доходе семьи: 100 – 67 – 6 = 27.

Ответ: заработок жены составляет 27%.

Задача 5. В свежих абрикосах 90% влаги, а в сухофрукте кураге только 5%. Сколько килограммов абрикосов нужно, чтобы получить 20 килограммов кураги?

Как решаем:

Исходя из условия, в абрикосах 10% питательного вещества, а в кураге в концентрированном виде — 95%.

Поэтому в 20 килограммах кураги 20 * 0,95 = 19 кг питательного вещества.

На вопрос задачи мы ответим, если разделим одинаковое количество питательного вещества, которое содержится в разных объемах свежих абрикосов и кураги, на его процентное содержание в абрикосах.

19 : 0,1 = 190

Ответ: 190 кг свежих абрикосов потребуется для изготовления 20 кг кураги.

Формулы для определения необходимой доли от суммы

Есть несколько способов найти требуемый процент от любого числа.

Первый способ состоит в делении нужной суммы на 100, после чего полученный результат умножается на % который необходимо определить.

Формула расчёта в данном случае выглядит так:

A / 100 * B =

В данной формуле A – это базовое число, из которого нужно извлечь долю.

B – процент, который необходимо высчитать в числовом выражении.

Например, в каком-либо магазине вам отдают товар, цена которого 500 рублей, за 70% его стоимости. Используя приведённую выше формулу, высчитываем, сколько нам необходимо заплатить в конечном итоге (или сколько будет 70% от 500 рублей):

500 / 100 * 70 = 350 рублей

Таким образом, мы сможем приобрести нужный товар за 350 рублей.

Второй способ состоит в умножении базового числа A на коофициент 0,B

Где А – это базовое число, а B – количество процентов, которые необходимо определить.

Формула имеет следующую форму:

A * 0,B =

В случае упомянутого выше примера с 70% стоимости от 500 высчитываем стоимость товара:

500 * 0,70 = 350

Третий способ состоит в умножении базового числа на количество процентов, после чего полученный результат делим на 100.

Формула выглядит следующим образом:

A * B  / 100 =

В нашем случае это:

500 * 70 / 100 = 350

На калькуляторе нужная доля от числа находится ещё проще:

1. Набираете на калькуляторе базовое число (А).
2. Жмёте на умножить, вводите искомое число процентов.
3. После чего жмёте на кнопку %, а затем на кнопку =. Калькулятор тот час же отобразит требуемый результат.

500*70% = (результат)

Расчет кредита на онлайн-калькуляторе

Сегодня кредитные онлайн-калькуляторы размещаются не только на сайтах банков, но и на большинстве специализированных интернет-ресурсов, посвященных финансовой тематике. Причина такой ситуации очевидна и заключается в удобстве и простоте пользования подобными инструментами.

Буквально в течение нескольких секунд любой желающий может рассчитать на кредитном калькуляторе онлайн примерные параметры доступного кредита. Примеры подобных расчетов приведены в таблице.

Исходные условия кредита	Результат расчета
Сумма	Срок	Ставка	Ежемесячный платеж, руб.	Величина переплаты, тыс. руб.	Общая сумма выплат, млн. руб.
450 тыс. руб.	Полгода	12%	77 647	15,785	0,466
500 тыс. руб.	Год	12%	44 424	32,978	0,533
1 млн. руб.	Год	18%	91 680	99,798	1,100
1,5 млн. руб.	2 года	15%	72 730	245,144	1,745
2 млн. руб.	Год	11%	176 763	120,744	2,121
3 млн. руб.	5 лет	11%	65 227	912,792	3,913
5 млн. руб.	5 лет	10%	106 235	1 372,894	6,373
5 млн. руб.	7 лет	10%	83 006	1 971,075	6,971

Возможность предварительно рассчитать кредит позволяет определить наиболее важные его параметры, к числу которых относятся: величина регулярной выплаты, сумма переплаты и общий размер платежей по займу в целом. Сравнение нескольких вариантов расчетов наглядно показывает, какой вариант кредитования наличными наиболее выгоден для потенциального заемщика.

Расчет процентов по кредиту

Ключевым параметром для сравнения различных кредитов выступает величина выплаченных процентов или, как часто называют этот показатель, сумма переплаты. Именно она, наряду с эффективной процентной ставкой, демонстрирует реальную выгодность того или иного банковского продукта для клиента. Ниже приводятся примеры расчетов разных кредитов, отсортированные по данному параметру.

Исходные условия кредита	Результат расчета
Сумма	Срок	Ставка	Размер переплаты	Ежемесячный платеж	Общая сумма выплат, млн. руб.
500 тыс. руб.	Год	10%	27 402 руб.	43 958 руб.	0,527
500 тыс. руб.	1,5 года	10%	40 433 руб.	30 029 руб.	0,540
750 тыс. руб.	Год	10%	41 102 руб.	65 937 руб.	0,791
1 млн. руб.	Год	10%	54 803 руб.	87 916 руб.	1,055
750 тыс. руб.	1,5 года	10%	60 650 руб.	45 043 руб.	0,811
1 млн. руб.	1,5 год	10%	80 866 руб.	60 057 руб.	1,081 млн. руб.

Расчет ежемесячного платежа по кредиту

Не менее серьезное значение в процессе выбора кредита выступает величина ежемесячной выплаты по нему. От величины этого параметра зависит, насколько серьезная финансовая нагрузка ляжет на заемщика. Ниже размещены примеры расчетов условий кредита наличными с выделением данного показателя

Исходные условия кредита	Результат расчета
Сумма	Срок	Ставка	Ежемесячный платеж	Величина переплаты	Общая сумма выплат, млн. руб.
500 тыс. руб.	2 года	10%	23 072 руб.	53 664 руб.	0,554
50 тыс. руб.	Год	12%	44 424 руб.	32 978 руб.	0,533
1 млн. руб.	2 года	10%	46 145 руб.	107 328 руб.	1,107
1 млн. руб.	Год	12%	88 849 руб.	65 957 руб.	1,066
3 млн. руб.	2 года	9,5%	137 743 руб.	305 420 руб.	3,305
5 млн. руб.	3 года	9,5%	160 165 руб.	765 069 руб.	5,795

Как найти процентное соотношение чисел

Также могут возникнуть ситуации, когда нужно высчитать процентное соотношение двух чисел. К примеру, какой процент число B составляет от числа А, на сколько процентов (B) вы выполнили свою работу от заданной нормы (A), на сколько (B) повысилась цена товара от первоначальной (A) и так далее.

Для определения такого результата существуют следующая формула:

B / A * 100 =

К примеру, нам нужно высчитать, какая доля от числа 500 составляет число 85.

Используя приведённую формулу, выполняем несложные арифметические операции:

85 / 500 * 100 = 17%

Таким образом, число 85 составляет 17% от 500.

Проверяем полученное число по формуле первого способа:

500 / 100 * 17 = 85.

Всё сошлось.

Расчет при помощи пропорций

Этот способ высчитывания известен всем со школьной программы.

Расчет применяют в случаях, когда необходимо высчитывать процентное соотношение между двумя данными. Иначе говоря, если одно число представляет собой 100%, то сколько будет составлять второе?

Например, Х (икс) – это 100%, Y – это n%. Для вычисления значения n необходимо записать пример в следующем виде:

X = 100.

Y = n.

Перемножив числа по диагоналям, получим пропорцию:

X*n = Y*100.

n = (Y*100)/X.

Пример.

Нужно посчитать, какую долю от 500 составят 25.

1. 500 = 100%, 25 = n%.
2. n = (25*100)/500 = 5%.

Обратите внимание: в этих случаях Y должно быть меньше Х, иначе результат получится больше 100%.

Если нужно получить число, которое составляет какую-либо часть, потребуется воспользоваться обратной формулой:

Y = (n*X)/100.

Пример.

Нужно подсчитать, сколько будет 5% от 500.

Y = (5*500)/100 = 25.

Расчет значения по методу соотношений

Востребованный людьми вариант, помогающий обеспечить расчет процентов, заключается в том, что следует использовать %, как десятичную дробь.

Соответственно, один процент будет выглядеть так — 0,01, то есть одна сотая. Записав себе % при помощи десятичной дроби, можно использовать великолепный инструмент, отлично подходящий для проведения вычислений.

Вам понадобиться умножить общее значение на число, соответствующее искомому проценту, указанное в виде десятичной дроби. Эта формула также поможет получить корректный результат математических вычислений.

Можно использовать свое значение процента в виде простой дроби. Выглядит это так: 1% равен 1/100

Если брать во внимание значение 10%, то его запишем в виде 1/10 и т.п

Узнать, каково значение 12,5% от суммы можно разделив ее на значение 8. Ниже рассмотрим практические примеры этого действия:

• 20% от суммы. Получается 1/5. То есть делим на значение 5;
• 25% от суммы. Понятно, что это четверть. Значит, производит деление на цифру 4;
• 50% — половина и т.д.

При использование калькулятора в расчетах процента годовых от общей суммы, не требуется нажимать знак равно. Электронная машина автоматически произведет вычисления, после нажатия на кнопку %.

Как высчитать процент из суммы с помощью пропорции

Но можно поступить и иначе. Для этого придется использовать знания о методе пропорций, который проходят в рамках школьного курса математики. Это будет выглядеть так.

Пусть у нас есть А — основная сумма, равная 100%, и В — сумма, соотношение которой с А в процентах нам нужно узнать. Записываем пропорцию:

А = 100

В = Х

Более полную информацию по теме вы можете найти в КонсультантПлюс.
Пробный бесплатный доступ к системе на 2 дня.

(Х в данном случае — число процентов).

По правилам расчета пропорций мы получаем следующую формулу:

Х = 100 * В / А

Если же нужно узнать, сколько будет составлять сумма В при уже известном числе процентов от суммы А, формула будет выглядеть по-другому:

В = 100 * Х / А

Теперь остается подставить в формулу известные числа — и можно производить расчет.

Подпишитесь на рассылку