Онлайн калькулятор для работы с комплексными числами

Понятие комплексного числа

Прежде чем, мы перейдем к рассмотрению комплексных чисел, дам важный совет: не пытайтесь представить комплексное число «в жизни» – это всё равно, что пытаться представить четвертое измерение в нашем трехмерном пространстве.

Если хотите, комплексное число – это двумерное число. Оно имеет вид , где  и  – действительные числа,  – так называемая мнимая единица. Число  называется действительной частью () комплексного числа , число  называется мнимой частью () комплексного числа .

 – это ЕДИНОЕ  ЧИСЛО, а не сложение. Действительную и мнимую части комплексного числа, в принципе, можно переставить местами:  или переставить мнимую единицу:  – от этого комплексное число не изменится. Но стандартно комплексное число принято записывать именно в таком порядке: 

Чтобы всё было понятнее, сразу приведу геометрическую интерпретацию. Комплексные числа изображаются на комплексной плоскости: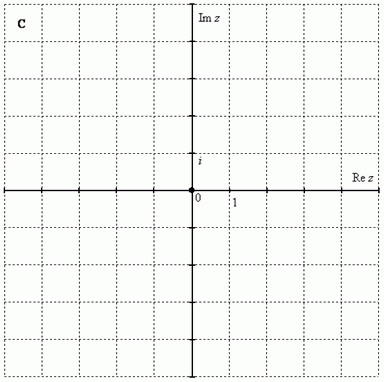
Как упоминалось выше, буквой  принято обозначать множество действительных чисел. Множество же комплексных чисел принято обозначать «жирной» или утолщенной буквой . Поэтому на чертеже следует поставить букву , обозначая тот факт, что у нас комплексная плоскость.

Комплексная плоскость состоит из двух осей: – действительная ось – мнимая ось

Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат (см. Графики и свойства элементарных функций). По осям нужно задать масштаб, отмечаем:

ноль;

единицу по действительной оси;

мнимую единицу  по мнимой оси.

Не нужно проставлять все значения: …–3, –2, –1, 0, 1, 2, 3,… и .

Да чего тут мелочиться, рассмотрим чисел десять.

Построим на комплексной плоскости следующие комплексные числа:, , , , , , ,

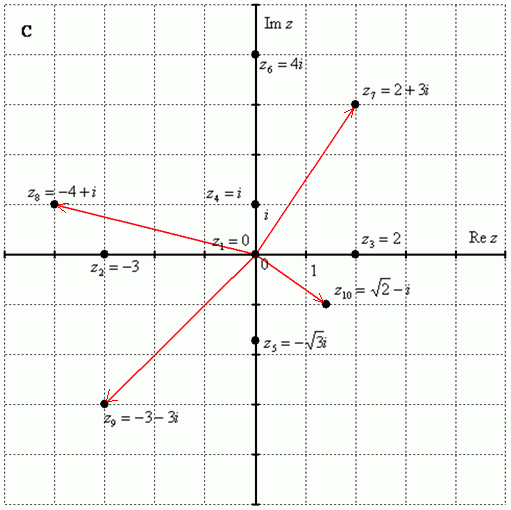
По какому принципу отмечены числа на комплексной плоскости, думаю, очевидно – комплексные числа отмечают точно так же, как мы отмечали точки еще в 5-6 классе на уроках геометрии.
Рассмотрим следующие комплексные числа: , , . Вы скажете, да это же обыкновенные действительные числа! И будете почти правы. Действительные числа – это частный случай комплексных чисел. Действительная ось  обозначает в точности множество действительных чисел , то есть на оси сидят все наши «обычные» числа. Более строго утверждение можно сформулировать так: Множество действительных чисел  является подмножеством множества комплексных чисел .

Числа , ,  – это комплексные числа с нулевой мнимой частью.

Числа , ,  – это, наоборот, чисто мнимые числа, т.е. числа с нулевой действительной частью. Они располагаются строго на мнимой оси .

В числах , , ,  и действительная и мнимая части не равны нулю. Такие числа тоже обозначаются точками на комплексной плоскости, при этом, к ним принято проводить радиус-векторы из начала координат (обозначены красным цветом на чертеже). Радиус-векторы к числам, которые располагаются на осях, обычно не  чертят, потому что они сливаются с осями.

Алгебраическая форма комплексного числа. Сложение, вычитание, умножение и деление комплексных чисел

С алгебраической формой комплексного числа мы уже познакомились,  – это и есть алгебраическая форма комплексного числа. Почему речь зашла о форме? Дело в том, что существуют еще тригонометрическая и показательная форма комплексных чисел, о которых пойдет речь в следующем параграфе.

Действия с комплексными числами не представляют особых сложностей и мало чем отличаются от обычной алгебры.

Сложение комплексных чисел

Пример 1

Сложить два комплексных числа ,

Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:

Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.

Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.

Для комплексных чисел справедливо правило первого класса:  – от перестановки слагаемых сумма не меняется.

Вычитание комплексных чисел

Пример 2

Найти разности комплексных чисел  и , если ,

Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:

Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .

Рассчитаем вторую разность:
Здесь действительная часть тоже составная:

Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.

Умножение комплексных чисел

Настал момент познакомить вас со знаменитым равенством:

Пример 3

Найти произведение комплексных чисел  ,

Очевидно, что произведение следует записать так:

Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что  и быть внимательным.

Повторим, omg, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.

Я распишу подробно:

Надеюсь, всем было понятно, что

Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках. Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство:

Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .

В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.

Деление комплексных чисел

Пример 4

Даны комплексные числа , . Найти частное .

Составим частное:

Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.

Вспоминаем бородатую формулу  и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть

Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :

Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой  (помним, что и не путаемся в знаках!!!).

Распишу подробно:

Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .

В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:

Редко, но встречается такое задание:

Пример 5

Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме ).

Приём тот же самый – умножаем знаменатель и числитель на сопряженное знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть , поэтому знаменатель и числитель нужно домножить на сопряженное выражение , то есть на :

Пример 6

Даны два комплексных числа , . Найти их сумму, разность, произведение и частное.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

На практике запросто могут предложить навороченный пример, где нужно выполнить много действий с комплексными числами. Никакой паники: будьте внимательны, соблюдайте правила алгебры, обычный алгебраический порядок действий, и помните, что

Реальный пример: Вращения

Мы не будем дожидаться университетского курса физики, чтобы попрактиковаться с комплексными числами. Мы займемся этим уже сегодня. Много можно рассказать на тему умножения комплексных чисел, но пока нужно понять главное:

Умножение на комплексное число совершает вращение на его угол

Давайте посмотрим, как это работает. Представьте, что я на лодке, движусь с курсом 3 единицы на Восток каждые 4 единицы на Север. Я хочу изменить свой курс на 45 градусов против часовой стрелки. Каким будет мой новый курс?

Кто-то может сказать «Это просто! Вычислите синус, косинус, погуглите значение по тангенсу…и тогда…» Кажется, я сломал свой калькулятор…

Давайте пойдем более простым путем: мы идем по курсу 3 + 4i (не важно, какой тут угол, нам всё равно пока) и хотим повернуться на 45 градусов. Ну, 45 градусов это 1 + i (идеальная диагональ)

Так что мы можем умножить наш курс на это число!

Вот в чем суть:

• Исходный курс: 3 единицы на Восток, 4 единицы на Север = 3 + 4i
• Вращение против часовой стрелки на 45 градусов = умножение на 1 + i

При умножении мы получаем:

Наш новый ориентир — 1 единица на Запад (-1 на Восток) и 7 единиц на Север, можете нарисовать координаты на графике и следовать им.

Но! Мы нашли ответ за 10 секунд, без всяких синусов и косинусов. Не было векторов, матриц, отслеживания, в каком квадранте мы находимся. Это была простая арифметика и немного алгебры для приведения уравнения. Мнимые числа отлично справляются с вращением!

Более того, результат такого вычисления очень полезен. У нас есть курс (-1, 7) вместо угла (atan(7/-1) = 98.13, и сразу ясно, что мы во втором квадранте. Как, собственно, вы планировали нарисовать и следовать указанному углу? Используя транспортир под рукой?

Нет, вы бы конвертировали угол в косинус и синус (-0.14 и 0.99), нашли бы примерное соотношение между ними (около 1 к 7) и набросали бы треугольник. И тут комплексные числа несомненно выигрывают — аккуратно, молниеносно, и без калькулятора!

Если вы похожи на меня, то это открытие покажется вам сногсшибательным. Если нет, боюсь, что математика вас совсем не зажигает. Уж извините!

Тригонометрия хороша, но комплексные числа значительно упрощают вычисления (вроде поиска cos(a + b)). Это только маленький анонс; в следующих статьях я предоставлю вам полное меню.

Лирическое отступление: некоторые люди думают примерно так: «Эй, ну не удобно же иметь курс Север/Восток вместо простого угла для следования судна!»

Правда? Ну хорошо, посмотрите на свою правую руку. Какой угол между основанием вашего мизинца и кончиком указательного пальца? Удачи с вашим способом вычисления.

А можно просто ответить «Ну, кончик находится на Х дюймов вправо и Y дюймов вверх» и с этим уже можно что-то сделать.

Аргумент комплексного числа

      Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа   z.

      Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором    z.

      Аргумент комплексного числа  z  считают положительным, если поворот от положительного направления вещественной оси к  радиус-вектору z  происходит против часовой стрелки, и отрицательным  — в случае поворота по часовой стрелке (см. рис.).

      Считается, что комплексное число нуль аргумента не имеет.

      Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где  k  — произвольное целое число, то вводится, главное значение аргумента, обозначаемое   arg z   и удовлетворяющее неравенствам:

      Тогда оказывается справедливым равенство:

      Если для комплексного числа   z = x + i y   нам известны его модуль   r = | z | и его аргумент φ, то мы можем найти вещественную и мнимую части по формулам

(3)

      Если же комплексное число   z = x + i y   задано в алгебраической форме, т.е. нам известны числа   x   и   y,   то модуль этого числа, конечно же, определяется по формуле

(4)

а аргумент определяется в соответствии со следующей Таблицей 1.

      Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом  k  обозначать в Таблице 1 произвольное целое число.

      Таблица 1. – Формулы для определения аргумента числа   z = x + i y

Расположениечисла  z	Знаки x и y	Главное значение аргумента	Аргумент	Примеры
Положительная вещественнаяполуось	x > 0 , y = 0	φ = 2kπ
	x > 0 , y > 0
Положительнаямнимаяполуось	x = 0 , y > 0
	x < 0 , y > 0
Отрицательнаявещественнаяполуось	x < 0 , y = 0	π	φ = π + 2kπ
	x < 0 , y < 0
Отрицательнаямнимаяполуось	x = 0 , y < 0
	x > 0 , y < 0

Расположениечисла  z	Положительнаявещественнаяполуось
Знаки x и y	x > 0 , y = 0
Главноезначениеаргумента
Аргумент	φ = 2kπ
Примеры

Расположениечисла  z
Знаки x и y	x > 0 , y > 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z	Положительнаямнимаяполуось
Знаки x и y	x = 0 , y > 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z
Знаки x и y	x < 0 , y > 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z	Отрицательнаявещественнаяполуось
Знаки x и y	x < 0 , y = 0
Главноезначениеаргумента	π
Аргумент	φ = π + 2kπ
Примеры

Расположениечисла  z
Знаки x и y	x < 0 , y < 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z	Отрицательнаямнимаяполуось
Знаки x и y	x = 0 , y < 0
Главноезначениеаргумента
Аргумент
Примеры

Расположениечисла  z
Знаки x и y	x < 0 , y < 0
Главноезначениеаргумента
Аргумент
Примеры

Расположение числа   z : Положительная вещественная полуось Знаки x и y : x > 0 ,   y = 0 Главное значение аргумента: Аргумент: φ = 2kπ Примеры:

Расположение числа   z : Знаки x и y : x > 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Положительная мнимая полуось Знаки x и y : x = 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Знаки x и y : x < 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Отрицательная вещественная полуось Знаки x и y : x < 0 ,   y = 0 Главное значение аргумента: π Аргумент: φ = π + 2kπ Примеры:

Расположение числа   z : Знаки x и y : x < 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Отрицательная мнимая полуось Знаки x и y : x = 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры:

Расположение числа   z : Знаки x и y : x < 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры:

Math Solution

Функциональный и удобный сервис, позволяющий выполнять сразу четыре  алгебраические операции: на сложение, вычитание, деление и умножение. Ознакомимся с основными рабочими этапами:

просмотрите правила ввода, кликнув на «+»;

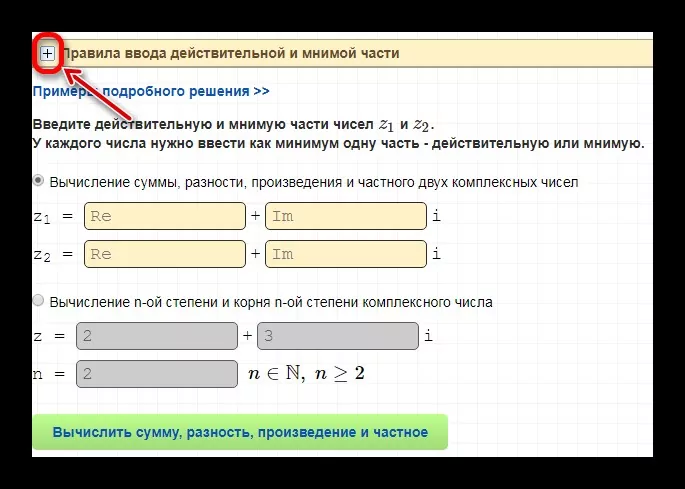
• введите необходимые значения;
• посчитайте, для этого есть специальная кнопка с вычислением;

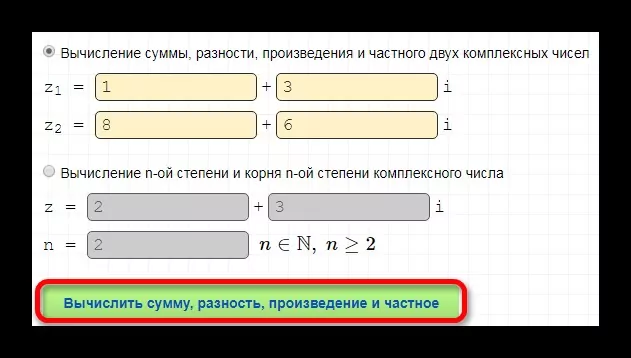
получите результат и подробное описание.

Этот ресурс станет настоящей находкой для старшеклассников. Легко заменит репетиторов и дорогие учебники. Подробное и понятное описание теории и принципов решения позволит быстро усвоить необходимый материал. Здесь вы не просто решаете задачи, используете онлайн калькулятор с подробным решением, но и можете легко понять, как это вычислялось.

Мир математики

Достойный внимания сайт, предоставляющий после полученного ответа подробные пояснения. Работать с ним также очень легко:

вводите условия в соответствующие поля;

• выбираете нужное действие;
• после нажатия на выбранную операцию будет начато вычисление и выдан результат.

Здесь вы найдете при необходимости подробную инструкцию для работы, так что точно не запутаетесь. Доступны разные варианты вычислительных сервисов, к примеру, матричный, инженерный и прочие.

Полезный контент:

• Формат heic, чем открыть, что это такое?
• Перевод с английского на русский с транскрипцией — лучшие онлайн сервисы
• Видеодрайвер перестал отвечать и был восстановлен — что за ошибка?
• Запись видео с экрана компьютера — какие программы в этом помогут?
• Караоке онлайн петь бесплатно с баллами — какие сервисы в этом помогут

Тригонометрический калькулятор онлайн — примеры

Как произвести онлайн расчет синусов и косинусов, тангенсов

Обратите внимание, что kalkpro.ru способен оперировать как градусами, так радианами и градами. 1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан

1 рад = 57,3°; 360° = 2π рад., 1 град = 0,9 градусов или 1 град = 0,015708 радиан.

Для включения того или иного режима измерения нажмите нужную кнопку:

где Deg – градусы, Rad – измерение в радианах, Grad — в градах. По умолчанию включен режим расчета в градусах.

В качестве самого простого примера найдем синус 90 градусов. Нажмите:

90

Ответ: единица

Также рассчитываются и другие тригонометрические функции, например, вычислим косинус 60 °:

60

Решение: 0,5

Аналогичным способом вычисляются обратные тригонометрические функции онлайн на КАЛКПРО — арксинус , арккосинус, арктангенс, а также гиперболические функции sinh, cosh, tanh.

Для их ввода необходимо переключить интерфейс, нажав , появятся новые кнопки – asin, acos, atan. Порядок ввода данных прежний: сначала величину, затем символ нужной функции, будь то акрсинус или арккосинус.

Преобразование с кнопкой Dms и Deg на калькуляторе

позволяет перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. производит обратный перевод – в формат «градусы; минуты; секунды».

Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды переведем в десятые доли:

35,140453 35,23459166666666666666

Переведем в прежний формат: 35,23459166666666666666 35,140453

Десятичный логарифм онлайн

Десятичный логарифм на калькуляторе рассчитывается следующим образом, например, ищем log единицы по основанию 10, log10(1) или lg1:

1

Получается 0 в итоге. Для подсчета lg100 нажмем так:

100

Решение: два. Как себя проверить? Что вообще такое десятичный логарифм — log по основанию 10. В нашем примере 2 – это степень в которую необходимо ввести основание логарифма, то есть 10, чтобы получить 100.

Так же вычисляется натуральный логарифм, но кнопкой .

Как пользоваться памятью на калькуляторе

Существующие кнопки памяти: M+, M-, MR, MS, MC.

Добавить данные в память программы, чтобы потом провести с ними дальнейшие вычисления поможет операция MS.

MR выведет вам на дисплей сохраненную в памяти информацию. MC удалит любые данные из памяти. M- вычтет число на онлайн дисплее из запомненного в памяти.

Пример. Внесем сто сорок пять в память программы:

145

После проведения других вычислений нам внезапно понадобилось вернуть запомненное число на экран электронного калькулятора, нажимаем просто:

На экране отобразится снова 145.

Потом мы снова считаем, считаем, а затем решили сложить, к примеру, 85 с запомненным 145, для этого нажимаем , либо для вычитания 85 из запомненного 145. В первом случае по возвращению итогового числа из памяти кнопкой получится 230, а во втором, после нажатия и получится 60.

Инженерный калькулятор kalkpro.ru быстро и точно проведет сложные вычисления, значительно упрощая ваши задачи.

Перечень калькуляторов и функционал будет расширяться, просто добавьте сайт в закладки и расскажите друзьям!

Комплекс операций инженерного калькулятора

Встроенный математический калькулятор поможет вам провести самые простые расчеты: умножение и суммирование, вычитание, а также деление. Калькулятор степеней онлайн быстро и точно возведет любое число в выбранную вами степень.

Представленный инженерный калькулятор содержит в себе все возможные вариации онлайн программ для расчетов. Kalkpro.ru содержит тригонометрический калькулятор (углы и радианы, грады), логарифмов (Log), факториалов (n!), расчета корней, синусов и арктангенсов, косинусов, тангенсов онлайн – множество тригонометрический функций и не только.

Работать с вычислительной программой можно онлайн с любого устройства, в каждом случае размер интерфейса будет подстраиваться под ваше устройство, либо вы можете откорректировать его размер на свой вкус.

Ввод цифр производится в двух вариантах:

• с мобильных устройств – ввод с дисплеем телефона или планшета, клавишами интерфейса программы
• с персонального компьютера – с помощью электронного дисплея интерфейса, либо через клавиатуру компьютера любыми цифрами

Ввод мнимых чисел

С мнимыми числами та же история. Мы можем решать уравнения вроде этого целыми днями:

Ответами будут 3 и -3. Но представим, что какой-то умник приписал сюда минус:

Ну и ну. Такой вопрос заставляет людей съеживаться, первый раз видя его. Вы хотите вычислить квадратный корень из числа, меньшего, чем ноль? Это немыслимо! (Исторически реально существовали подобные вопросы, но мне удобнее представлять какого-то безликого умника, чтобы не вгонять в краску ученых прошлого).

Выглядит безумно, как в свое время выглядели и отрицательные числа, ноль и иррациональные числа (неповторяющиеся числа). В этом вопросе нет «реального» смысла, правда?

Нет, не правда. Так называемые «мнимые числа» нормальны настолько же, как и все другие (или настолько же ненормальные): они являются инструментом для описания мира. В том же духе, как мы представляем, что -1, 0.3 и 0 «существуют», давайте предположим, что существует некое число i, где:

Другими словами, вы умножаете i на себя же, чтобы получить -1. Что сейчас происходит?

Ну, сначала у нас конечно болит голова. Но, играя в игру «Давайте представим, что i существует», мы действительно делаем математику проще и элегантнее. Появляются новые связи, которые мы с легкостью можем описать.

Вы не поверите в i, как и те старые математики-ворчуны не верили в существовании -1. Все новые, сворачивающие мозг в трубочку понятия сложны для восприятия, и их смысл вырисовывается не сразу, даже для гениального Эйлера. Но, как показали нам отрицательные числа, странные новые идеи могут быть чрезвычайно полезными.

Я не люблю сам термин «мнимые числа» — такое чувство, что он был выбран специально, чтобы оскорбить чувства i. Число i такое же нормальное, как и другие, но за ним закрепилась кличка «мнимое», так что мы тоже будем ей пользоваться.

Как пользоваться инженерным калькулятором – на примерах

Как возвести в степень

Чтобы возвести, к примеру, 12^3 вводите в следующей последовательности:

12 3

12, клавиша «икс в степени игрик» , 3, знак равенства

Ответ: 1728

Как найти корень кубический

Допустим, что мы извлекаем корень кубический из 729, нажмите в таком порядке:

729

729, «кубический корень из икс», равенства

Как найти корень на калькуляторе

Задача: Найти квадратный корень 36.

Решение: всё просто, нажимаем так:

36 y√x] 2

36, «корень из икса, в степени игрик», нужную нам степень 2, равно

Ответ: 6

При помощи этой функции вы можете найти корень в любой степени, не только квадратный.

Как возвести в квадрат

Для возведения в квадрат онлайн вычислительная программа содержит две функции:

«икс в степени игрик», «икс в квадрате»

Последовательность ввода данных такая же, как и раньше – сначала исходную величину, затем «x^2» и знак равно, либо если не квадрат, а произвольное число, необходимо нажать функцию «x^y», затем указать необходимую степень и так же нажать знак «равно».

Например: 45 6

Ответ: сорок пять в шестой степ. равно 8303765625

Эпилог: Но они по-прежнему довольно странные!

Я знаю, они и для меня всё еще выглядят странными. Я пытаюсь мыслить, как мыслил первый человек, открывший ноль.

Ноль — это такая странная идея, «что-то» представляет «ничего», и это никак не могли понять в Древнем Риме. То же самое и с комплексными числами — это новый способ мышления. Но и ноль, и комплексные числа значительно упрощают математику. Если бы мы никогда не внедряли странности вроде новых систем счисления, мы бы до сих пор считали всё на пальцах.

Я повторяю эту аналогию, потому что так легко начать думать, что комплексные числа «не нормальные». Давайте быть открытыми к новшествам: в будущем люди будут только шутить над тем, как кто-то вплоть до XXI века не верил в комплексные числа.

Перевод статьи «A Visual, Intuitive Guide to Imaginary Numbers»

Поиск множеств

Давайте углубимся немного в детали. При умножении отрицательных чисел (как -1), вы получаете множество:

1, -1, 1, -1, 1, -1, 1, -1

Поскольку -1 не меняет размер числа, а только знак, вы получаете одно и то же число то со знаком «+», то со знаком «-». Для числа х у вас получится:

x, -x, x, -x, x, -x…

Это очень полезная мысль. Число «х» может представлять хорошие и плохие недели. Представим, что хорошая неделя сменяет плохую; это хорошая неделя; а какой будет 47-я неделя?

-x означает, что неделя выдастся плохой. Видите, как отрицательные числа «следят за знаком» — мы можем просто ввести (-1)^47 в калькуляторе вместо того, чтобы считать («Неделя 1 хорошая, неделя 2 плохая… неделя 3 хорошая…»). Вещи, которые постоянно чередуются можно отлично смоделировать, используя отрицательные числа.

Хорошо, а что будет, если мы продолжим умножать на i?

Очень смешно, давайте немного это всё упростим:

• (Тут вопросов быть не может)
• (Тут я тоже мало что могу)
• (В этом всё i)
• (Ага, 3 оборота против часовой стрелки = 1 оборот по часовой стрелке. Всё четко)
• (4 оборота дают в сумме «полный круг»)
• (И снова по кругу…)

Вот всё то же представлено графически:

Мы повторяем цикл каждый 4-й поворот. В этом определенно есть смысл, да? Любой ребенок скажет вам, что 4 поворота влево — это всё равно, что не поворачиваться вовсе. А теперь оторвитесь от мнимых чисел (i, i^2)и посмотрите на общее множество:

X, Y, -X, -Y, X, Y, -X, -Y…

Точно, как отрицательные числа моделируют зеркальное отражение чисел, мнимые числа могут моделировать что угодно, что вращается между двумя измерениями «Х» и «Y». Или что угодно с циклической, круговой зависимостью — есть что-нибудь на примете?

Сопряженные числа и их свойства

Пусть —
комплексное число. Число ,
отличающееся от числа лишь знаком
при мнимой части, называется числом, сопряжённым с .

Свойства сопряжённых чисел

1) (число,
сопряжённое сопряжённому числу, равно данному числу);

2) если и —
комплексные числа, то и
(число, сопряжённое
с суммой двух чисел, равно сумме чисел, сопряжённых со слагаемыми и число, сопряжённое с
произведением, равно произведению чисел, сопряжённых с сомножителями).

3) если ,
то и
— положительное
действительное число, равное нулю тогда и только тогда, когда ,
т. е. когда и
.

Пример 8. Даны комплексные числа
и
. Убедиться
в справедливости свойств сопряжённых чисел.

Решение. Сопряжёнными данным комплексным числам являются числа
и . Сумма данных комплексных чисел:

,

а произведение:

.

В свою очередь

,

Таким образом, справедливость свойств сопряжённых чисел доказана.