Сетевой график, пример построения
Содержание:
Методы оптимизации сетевого графика
Сетевой график проектной реализации связан с содержанием уникальной задачи, параметрами времени и пространства, в которых выполняется проект. Данной деятельности присущи все традиционные функции управления без исключения. С этой точки зрения процесс можно разделить на этапы, в которых весомую долю занимает планирование. Далее вашему вниманию представляется упрощенная блок-схема функциональных этапов управления проектом.
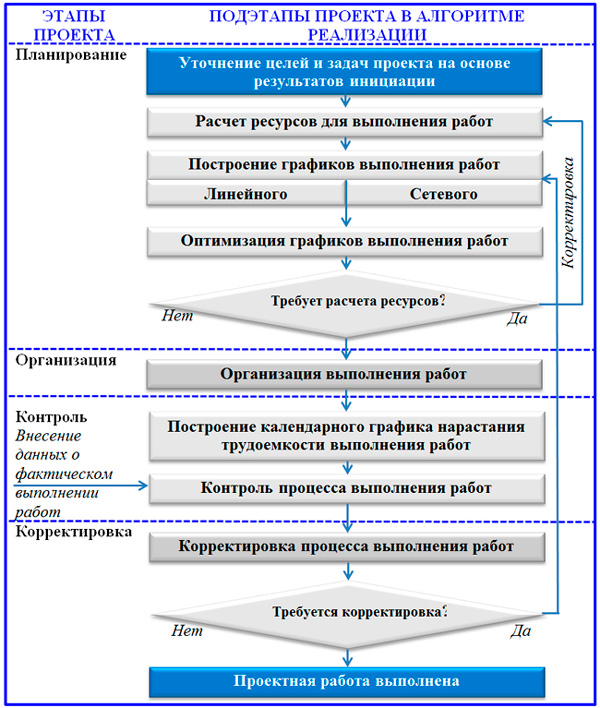 Функционально-процессная блок-схема управления проектом
Функционально-процессная блок-схема управления проектом
На текущий момент нас интересует оптимизация сетевого графика как подэтап процесса планирования проектной задачи. Это связано с тем, что после сбора информации о работах и ограничениях разработка визуальной модели в форме сетевой диаграммы подразумевает дальнейшее ее улучшение с использованием методов расчета расписания. Основных методов два: метод критического пути (сокращенно МКП) и анализ расписания по методу PERT.
При использовании МКП производится последовательный расчет наиболее ранних и самых поздних сроков работ по проекту. Далее устанавливается размер полного резерва, при этом критическими работами считаются действия, имеющие нулевой полный резерв. Наконец, рассчитываются временные резервы для выполнения операций, и в качестве самого длинного пути сети выбирается критический путь. Критических путей может быть несколько. Оптимизация сетевого графика методом критического пути применяется для следующих моделей диаграммы:
- для моделей с дискретным и непрерывным временем;
- для моделей с простым отношением предшествования;
- в сетях с обобщенными связями.
Метод оценки и анализа программ (PERT) служит вторым методом, по которому проводится оптимизация сетевого графика. Его основные отличия от МКП основаны на допущении, что длительность работ носит случайный характер, и для целей оценки и анализа сроков следует учитывать неопределенность временного параметра работ проекта. Также делается допущение о независимости всех случайных величин продолжительности критического пути. Для этих целей на основе метода математической статистики и теории вероятности используется β-распределение и оценка параметров распределения с трех экспертных позиций: оптимистичной, пессимистичной и наиболее вероятной.
Корректировка сетевого графика и сокращение общей продолжительности проекта входят в состав ключевых задач проект-менеджера. МКП дает возможность рассчитать оптимальные сроки выполнения проекта, но не позволяет найти инструменты для более действенного сокращения его продолжительности. В этом отношении метод критического пути не обладает достаточной гибкостью. Метод PERT также не лишен недостатков. Во-первых, он нацеливает в основном на оптимистический вариант оценки, во-вторых, PERT в меньшей степени применим к небольшим проектным задачам.
Для эффективной корректировки лучше всего подходят такие современные методы, как метод критической цепи и методы сжатия
Им мы намерены уделить внимание в отдельной статье. Все названные модели и методы являются предметной зоной компетенций PM, владея которыми, менеджеру проще демонстрировать свою эффективность, достигая результата проекта в условиях временных и ресурсных ограничений
Основные правила построения сетевого графика
Итак, основные правила построения сетевого графика сводятся к следующему:
Направление стрелок в сетевом графике следует принимать слева направо.
Форма графика должна быть простой, без лишних пересечений, большинство работ следует изображать горизонтальными линиями.
При выполнении параллельных работ, т.е
если одно событие служит началом двух работ или более, заканчивающихся другим событием, вводится зависимость и дополнительное событие, иначе разные работы будут иметь одинаковый код.
Если те или иные работы начинаются после частичного выполнения предшествующей, то эту работу следует разбить на части.
Если после окончания двух работ А и Б можно начать работу В, а начало работы, Г зависит только от окончания работы А и начало работы Д – от окончания работы Б, то на сетевом графике это изображается с помощью зависимостей.
При изображении поточных работ особое внимание уделяется правильной разбивке работ на захватки и выявлению взаимосвязи смежных работ.
Укрупнение сетей производится с соблюдением следующих правил:
группа работ на сетевом графике может изображаться как одна работа, если в этой группе имеется одно начальное и одно конечное событие;
укрупнять в одну работу следует только такие работы, которые закреплены за одним исполнителем (бригадой, участком и т.д.);
в укрупненную сеть нельзя вводить новые события, которых не было на более детальном графике до укрупнения;
наименование работ в укрупненном графике должно быть увязано с наименованием укрупняемых работ;
коды событий, которые сохраняются в укрупненном графике, должны быть такими же, как и в детальном графике.
При построении сетевого графика могут быть следующие ошибки. В сетевом графике не должно быть «тупиков», «хвостов» и «циклов»
«Тупик» — событие (кроме завершающего), из которого не выходит ни одна работа, «хвост» — событие (кроме исходного), в которое не входит ни одна работа, «цикл» — замкнутый контур, в котором работы возвращаются к тому событию, из которого они вышли.
Изображение поставок и других внешних работ осуществляется следующим образом. Работы, которые предшествуют выполнению тех или иных работ сетевого графика, но организационно решаются на другом уровне, называются внешними работами. К внешним работам можно отнести поступления технической документации, поставку материалов или оборудования, завоз строительных машин и т.д. Обычно такие работы графически выделяются, например, утолщенной стрелкой с двойным кружком.
Нумерация (кодирование) событий должна соответствовать последовательности работ во времени, т.е. предшествующим событиям присваиваются меньшие номера. Нумерацию событий рекомендуется производить только после окончательного построения сети и вести от исходного события, которому присваивается нулевой или первый номер. Последующее событие нельзя нумеровать, если не пронумеровано предшествующее ему событие. Кодирование можно вести горизонтальным или вертикальным методом. При горизонтальном методе события кодируют слева направо по прямым до первого пересечения работ. При вертикальном способе нумерацию начинают сверху вниз и снизу вверх с учетом условия: последующее событие получает номер после предыдущего.
Масштабный сетевой график
- Вычислить табличным методом все основные характеристики работ и событий, найти критический путь и его продолжительность.
- Построить масштабный сетевой график.
- Оценить вероятность выполнения всего комплекса работ за 30 дней.
- Оценить максимально возможный срок выполнения всего комплекса работ с вероятностью 95%.
| Код работы ( i,j) | Продолжительность | |
| tmin (i,j) | tmax (i,j) | |
| 1,2 | 5 | 10 |
| 1,4 | 2 | 7 |
| 1,5 | 1 | 6 |
| 2,3 | 2 | 4,5 |
| 2,8 | 9 | 19 |
| 3,4 | 1 | 3,5 |
| 3,6 | 9 | 19 |
| 4,7 | 4 | 6,5 |
| 5,7 | 2 | 7 |
| 6,8 | 7 | 12 |
| 7,8 | 5 | 7,5 |
Решение находим с помощью сервиса Сетевая модель
. В нашем задании продолжительность выполнения работы задаётся двумя оценками – минимальная и максимальная. Минимальная оценка характеризует продолжительность выполнения работы при наиболее благоприятных обстоятельствах, а максимальная tmax(i,j) – при наиболее неблагоприятных условиях. Продолжительность работы в этом случае рассматривается, как случайная величина, которая в результате реализации может принять любое значение в заданном интервале. Такие оценки называются вероятностными (случайными), и их ожидаемое значение tож(i,j) оценивается по формуле
tож(i,j)=(3 tmin(i,j)+2 tmax (i,j))/5
Для характеристики степени разброса возможных значений вокруг ожидаемого уровня используется показатель дисперсии:
S2(i,j)=0,04(tmax(i,j)-tmin(i,j))2Рассчитаем ожидаемое значение и показатель дисперсии.
tож(1,2)=(3*5+2*10)/5=7
tож(1,4)=(3*2+2*7)/5=4
tож(1,5)=(3*1+2*6)/5=3
tож(2,3)=(3*2+2*4,5)/5=3
tож(2,8)=(3*9+2*19)/5=13
tож(3,4)=(3*1+2*3,5)/5=2
tож(3,6)=(3*9+2*19)/5=13
tож(4,7)=(3*4+2*6,5)/5=5
tож(5,7)=(3*2+2*7)/5=4
tож(6,8)=(3*7+2*12)/5=9
tож(7,8)=(3*5+2*7,5)/5=6
S2(1,2)=0,04*(10-5)2=1
S2(1,4)=0,04*(7-2)2=1
S2(1,5)=0,04*(6-1)2=1
S2(2,3)=0,04*(4,5-1)2=0,25
S2(2,8)=0,04*(19-9)2=4
S2(3,4)=0,04*(3,5-1)2=6,25
S2(3,6)=0,04*(19-9)2=4
S2(4,7)=0,04*(6,5-4)2=0,25
S2(5,7)=0,04*(7-2)2=1
S2(6,8)=0,04*(12-7)2=1
S2(7,8)=0,04*(7,5-5)2=0,25
Полученные данные занесем в таблицу.
Таблица – Сетевая модель.
| Работа ( i,j) | Продолжительность | Ожидаемая продолжительность tож(i,j) | Дисперсия S2(i,j) | |
| tmin (i,j) | tmax (i,j) | |||
| 1,2 | 5 | 10 | 7 | 1 |
| 1,4 | 2 | 7 | 4 | 1 |
| 1,5 | 1 | 6 | 3 | 1 |
| 2,3 | 2 | 4,5 | 3 | 0,25 |
| 2,8 | 9 | 19 | 13 | 4 |
| 3,4 | 1 | 3,5 | 2 | 6,25 |
| 3,6 | 9 | 19 | 13 | 4 |
| 4,7 | 4 | 6,5 | 5 | 0,25 |
| 5,7 | 2 | 7 | 4 | 1 |
| 6,8 | 7 | 12 | 9 | 1 |
| 7,8 | 5 | 7,5 | 6 | 0,25 |
| КПР | Код работы (i,j) | Продолжительность работы t(i, j) | Ранние сроки | Поздние сроки | Резервы времени | |||
| tрн(i,j) | tро(i,j) | tпн(i,j) | tпо(i,j) | Rп | Rc | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1,2 | 7 | 7 | 7 | |||||
| 1,4 | 4 | 4 | 17 | 21 | 17 | 8 | ||
| 1,5 | 3 | 3 | 19 | 22 | 19 | |||
| 1 | 2,3 | 3 | 7 | 10 | 7 | 10 | ||
| 1 | 2,8 | 13 | 7 | 20 | 19 | 32 | 12 | 12 |
| 1 | 3,4 | 2 | 10 | 12 | 19 | 21 | 9 | |
| 1 | 3,6 | 13 | 10 | 23 | 10 | 23 | ||
| 2 | 4,7 | 5 | 12 | 17 | 21 | 26 | 9 | |
| 1 | 5,7 | 4 | 3 | 7 | 22 | 26 | 19 | 10 |
| 1 | 6,8 | 9 | 23 | 32 | 23 | 32 | ||
| 2 | 7,8 | 6 | 17 | 23 | 26 | 32 | 9 | 9 |
кр
P(tкр
где Z=(Т-Ткр)/SкрZ- нормативное отклонение случайной величины, Sкр – среднеквадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути.
Соответствие между Z и Ф(Z) представлено в таблице.
Таблица — Таблица стандартного нормального распределения.
| Z | F(Z) | Z | F(Z) | Z | F(Z) |
| 0.0000 | 1.0 | 0.6827 | 2.0 | 0.9643 | |
| 0.1 | 0.0797 | 1.1 | 0.7287 | 2.1 | 0.9722 |
| 0.2 | 0.1585 | 1.2 | 0.7699 | 2.2 | 0.9786 |
| 0.3 | 0.2358 | 1.3 | 0.8064 | 2.3 | 0.9836 |
| 0.4 | 0.3108 | 1.4 | 0.8385 | 2.4 | 0.9876 |
| 0.5 | 0.3829 | 1.5 | 0.8664 | 2.5 | 0.9907 |
| 0.6 | 0.4515 | 1.6 | 0.8904 | 2.6 | 0.9931 |
| 0.7 | 0.5161 | 1.7 | 0.9104 | 2.7 | 0.9949 |
| 0.8 | 0.5763 | 1.8 | 0.9281 | 2.8 | 0.9963 |
| 0.9 | 0.6319 | 1.9 | 0.9545 | 2.9 | 0.9973 |
Критический путь проходит по работам (1,2)(2,3)(3,6)(3,8).
Дисперсия критического пути:
S2(Lкр)= S2(1,2)+ S2(2,3)+ S2(3,6)+S2(6,8)=1+0,25+4+1=6,25
S(Lкр)=2,5
p(tкр<30)=0,5+0,5Ф((30-32)/2,5)=0,5-0,5Ф(0,8) = 0,5-0,5*0,5763=0,5-0,28815=0,213
Вероятность того, что весь комплекс работ будет выполнен не более чем за 30 дней, составляет 21,3%.
Для определения максимально возможного срока выполнения всего комплекса работ с надежностью 95% будем использовать следующую формулу:
Для решения поставленной задачи найдем значение аргумента Z, которое соответствует заданной вероятности 95% (значению графы Ф(Z) 0,9545*100% в таблице 5 соответствует Z=1,9).
T=32+1,9*2,5=36,8
Максимальный срок выполнения всего комплекса работ при заданном уровне вероятности 95% составляет всего 36,8 дня.
Построение матрицы
Перед тем как сформировать сетевой график, необходимо создать матрицу. Построение графиков начинается с этого этапа. Представим себе систему координат, в которой вертикальные значения соответствуют i (начальное событие), а горизонтальные строки – j (завершающее событие).
Начинаем заполнять матрицу, ориентируясь на данные рисунка 1. Первая работа не имеет времени, поэтому ею можно пренебречь. Рассмотрим детальнее вторую.
Начальное событие стартует с цифры 1 и заканчивается на втором событии. Продолжительность действия равняется 30 дням. Это число заносим в ячейку на пересечении 1 строки и 2 столбца. Аналогичным способом отображаем все данные, что представлено на рисунке ниже.
Автоматическая сетевая диаграмма проекта с критическим путем в EXCEL
Построим автоматическую сетевую диаграмму проекта. Сетевую диаграмму изобразим на диаграмме MS EXCEL типа Точечная. На этой диаграмме выведем работы проекта в виде точек, стрелками изобразим связи между работами. Также изобразим на диаграмме критический(ие) путь(и). Сетевая диаграмма будет автоматически перестраиваться при изменении связей между работами и их длительности.
Данная статья является третьей статьей в цикле статей посвященных построению сетевой диаграммы проекта и является синтезом первых двух:
- В статье Метод критического пути в MS EXCEL показано как рассчитать длительность проекта, определить работы на критическом пути и как построить сетевую диаграмму проекта на листе MS EXCEL. Основной недостаток – при изменении связей между работами пользователю потребуется вносить серьезное изменение в сетевую диаграмму.
- В статье Автоматическая сетевая диаграмма проекта в MS EXCEL показано, как имея перечень работ и связи между ними, вычислить все пути проекта и отобразить их на стандартной диаграмме типа Точечная. При изменении связей – пути автоматически пересчитываются. Однако, критический путь не вычислялся в этой статье.
Рекомендуется прочитать вышеуказанные статьи перед первым прочтением.
Ниже показана диаграмма, которую мы будем создавать в этой статье. На диаграмме отображены все работы проекта (от А до U, синие точки), связи между ними (стрелки), работы на критическом пути (красные точки), критический путь (красные стрелки).
Примечание : Слово диаграмма используется в 2-х смыслах: сетевая диаграмма проекта (стандартный термин из управления проектом, Activity-on-node diagram ) и диаграмма MS EXCEL ( Excel Chart , см. вкладку , группа ). Диаграмма MS EXCEL типа Точечная будет использоваться для построения сетевой диаграммы проекта.
При изменении связей между работами и/или их длительности происходит перерасчет критического пути и сетевая диаграмма автоматически обновляется. Например, значительное увеличение длительности работы М (в нижнем пути сетевой диаграммы) приведет к изменению критического пути.
Такая сетевая диаграмма отображает критический путь даже нагляднее, чем стандартная диаграмма Ганта , хотя, конечно, не заменяет ее.
ВНИМАНИЕ! Построение данной сетевой диаграммы в этой статье приведено лишь с целью демонстрации технической реализуемости такого построения в MS EXCEL. Не ставилось целью сделать “удобную программу для пользователей”
Это означает, что при изменении пользователем количества работ/ добавления связей между работами (например, использования более 5 последователей), переименовании листов, рядов диаграммы и других изменений, в файле примера может потребоваться дополнительная настройка формул.
Такая настройка потребует от пользователя серьезных знаний MS EXCEL и времени.
Исходная информация
В качестве исходной информации дан перечень работ, их длительность и связи между работами.
Также вручную задаются координаты для отображения на диаграмме работ (диапазон ВА12:ВВ34 ).
Другой информации для построения сетевой диаграммы и вычисления критического пути не требуется.
Вычисление путей сетевой диаграммы
Как и в статье Автоматическая сетевая диаграмма проекта в MS EXCEL начнем построение сетевой диаграммы с вычисления путей.
В отличие от указанной статьи, здесь увеличено количество рассчитываемых путей (до 15) и максимальная длина путей (до 10 работ, включая вехи начала и окончания).
Алгоритм вычисления путей аналогичен, однако формулы изменены, чтобы позволить пользователю быстро увеличивать количество путей проекта и их длину.
Начиная с шага №1 (начиная со строки 96) формулы можно копировать вниз и вправо, чтобы при необходимости увеличить количество путей и их длину (количество шагов). На каждом шаге длина путей увеличиваются на одну работу. В случае наличия нескольких последователей у работы – увеличивается количество возможных путей.
После вычисления всех шагов, в диапазоне R62:AA76 выводится перечень всех путей проекта, содержащие входящие в них работы.
Построение сетевой диаграммы
Сначала на диаграмме выводятся работы (синие точки, ряд Работы ).
Затем выводятся все возможные пути проекта (ряды Путь_1, Путь_2, …, Путь_15 ).
Все работы, находящиеся на критическом пути, отмечаются красным цветом. Также на диаграмму выводится критический путь. Если путей несколько, то выводятся все пути (в файле примера выводятся максимум 3 критических пути). Если длительность работы О увеличить до 8 дней, то 3 пути станут критическими с длительностью по 65 дней.
Одновременно, работы проекта отображаются на диаграмме Ганта.
Использование табличного метода
Общепризнанные ПП календарного планирования (MS Project, Primavera Suretrack, OpenPlan и т.п.) способны вычислять ключевые параметры сетевой модели проекта. Мы же в настоящем разделе табличным методом выполним настройку подобного расчета обычными средствами MS Excel. Для этого возьмем наш пример фрагмента проектных операций проекта в области СМР. Расположим основные параметры сетевого графика в столбах электронной таблицы.
Модель расчета параметров сетевого графика табличным способом
Преимуществом выполнения расчетов табличным способом является возможность простой автоматизации вычислений и избежание массы ошибок, связанных с человеческим фактором. Красным цветом будем выделять номера операций, располагающихся на критическом пути, а синим цветом отметим расчетные позиции частных резервов, превышающих нулевое значение. Разберем пошагово расчет параметров сетевого графика по основным позициям.
- Ранние начала операций, следующих за текущей работой. Алгоритм расчета настраиваем на выбор максимального значения из раннего времени окончания нескольких альтернативных предыдущих действий. Взять, например, операцию под номером 13. Ей предшествуют работы 6, 7, 8. Из трех ранних окончаний (71, 76, 74 соответственно) нам нужно выбрать максимальное значение – 76 и проставить его в качестве раннего начала операции 13.
- Критический путь. Выполняя процедуру расчета по пункту 1 алгоритма, мы доходим до конца фрагмента, найдя значение продолжительности критического пути, которая в нашем примере составила 120 дней. Значения наибольших ранних окончаний среди альтернативных действий обозначают операции, лежащие на критическом пути. Отмечаем эти операции красным цветом.
- Поздние окончания операций, предшествующих текущей работе. Начиная с концевой работы начинаем движение в обратную сторону от действий с большими номерами к операциям с меньшими. При этом из нескольких альтернатив исходящих работ выбираем наименьшее знание позднего начала. Поздние начала вычисляем как разницу между выбранными значениями поздних окончаний и продолжительности операций.
- Резервы операций. Вычисляем полные (общие) резервы как разницу между поздними началами и ранними началами либо между поздними окончаниями и ранними окончаниями. Значения частных (свободных) резервов получаем в результате вычитания из числа раннего начала следующей операции раннего окончания текущей.
Мы рассмотрели практические механизмы составления сетевого графика и расчета основных параметров временной продолжительности проекта. Таким образом, вплотную приблизились к исследованию возможностей анализа, проводимого с целью оптимизации сетевой модели и формирования непосредственно плана действий по улучшению ее качества. Настоящая тема занимает немного места в комплексе знаний проект-менеджера и не так уж и сложна для восприятия. Во всяком случае, каждый РМ обязан уметь воспроизводить визуализацию графика и выполнять сопутствующие расчеты на хорошем профессиональном уровне.
Глоссарий разработки сетевого графика
Построение сетевого графика методологически основано на общей концепции СПУ (системы планирования и управления) проектов. Ключевые аспекты данной методологии были рассмотрены в статье на тему сетевого планирования проекта. В настоящем материале мы развиваем начатое осмысление теоретических и прикладных вопросов сетевого моделирования. В первую очередь, нас интересует разработка сетевой диаграммы вида «вершина – работа» в контексте ее составления, оптимизации и корректировки. Логика сетевого планирования достаточно проста, математически метод не сложен.
Тем не менее, на практике применить полноценно эту модель удается не всегда. Возникают затруднения, во многом определяемые психологией участников, не готовых объективно рассчитать сроки исполнения сформулированных задач. Данный метод дает более слабый результат в условиях перегруженности ответственных ресурсов по проектным задачам. Сетевые графики хорошо работают в проектах, где ответственные исполнители заняты только на одном проекте, например, в строительстве. Ниже показана модель процесса календарного планирования, которая служит направляющим ориентиром в работе со средством планирования «сетевой график».
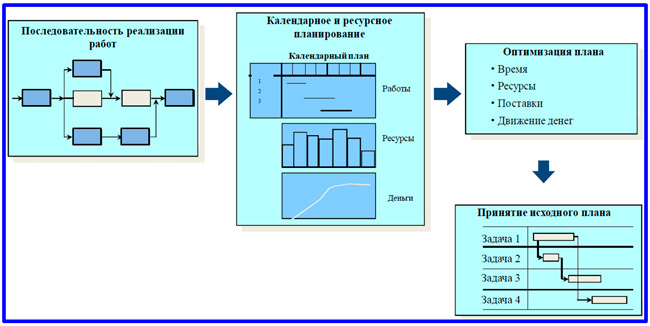 Схема разработки календарного плана проекта
Схема разработки календарного плана проекта
Введем основные понятия, которые понадобятся для составления сетевой модели проекта и ее оптимизации:
отношение предшествования – это характеристика связи последующей работы в отношении предшествующей;
путь – это непрерывная последовательность операций (работ) в сетевом графике;
предшествующий путь – участок полного пути от исходного до рассматриваемого события;
последующий путь – участок полного пути от рассматриваемого события до любого следующего;
критический путь – это полный путь, характеризуемый нулевым резервом;
критическая работа – действие, для которого полный резерв имеет нулевое значение;
предкритическая работа – операция, для которой менеджер проекта установил число предельного значения полного резерва;
резерв пути – разница между временной длительностью проекта и длиной пути на графике;
веха – работа с нулевой продолжительностью, обозначает важное, значимое событие в проекте;
минимальное время от начала проекта до начала выполнения операции без нарушения отношения предшествования называется ранним сроком начала работы;
максимальное время с начала проекта до начала выполнения операции, которое позволяет проекту закончиться вовремя без нарушения отношения предшествования, называется поздним сроком начала работы;
минимальное время, которое требуется для выполнения всех работ без нарушения отношения предшествования, называется ранним окончанием проекта;
возобновляемый ресурс предполагает ограничение в использовании его на каждом шаге планируемого периода;
невозобновляемый ресурс предполагает ограничение в использовании его на всем периоде реализации проекта.
Построение сетевого графика
В нашем примере для построения сетевого графика необходимо составить формуляр операций, его можно использовать в качестве образца на практике.
В таблицу сведем следующие данные по каждой операции:
- номер операции;
- предшествующие операции;
- количество исполнителей;
- продолжительность операции в днях.
В таблице операций их номера соответствует нумерации в карточке-определителе в соответствии с группировкой параллельных операций.
|
Номер операции |
Предыдущие операции |
Кол-во исполнителей, чел. |
Продолжительность, дни |
|---|---|---|---|
|
1. |
— |
10 |
1 |
|
2. |
1 |
2 |
3 |
|
3. |
1 |
3 |
1 |
|
4. |
1 |
2 |
4 |
|
5. |
4 |
1 |
0,5 |
|
6. |
3 |
3 |
2 |
|
7. |
5 |
2 |
0,5 |
|
8. |
2,7,6 |
10 |
0,5 |
|
9. |
9 |
10 |
0,5 |
|
10. |
9 |
1 |
3 |
|
11. |
9 |
2 |
4 |
|
12. |
9 |
2 |
2 |
|
13. |
9 |
2 |
3 |
|
14. |
12 |
2 |
2 |
|
15. |
13 |
3 |
2 |
|
16. |
10,11,14,15 |
10 |
0,5 |
|
17. |
16 |
10 |
0,5 |
|
18. |
17 |
2 |
2 |
|
19. |
18 |
2 |
3 |
|
20. |
17 |
2 |
2 |
|
21. |
17 |
2 |
3 |
|
22. |
21 |
3 |
1 |
|
23. |
20 |
2 |
2 |
|
24. |
19,22,23 |
10 |
0,5 |
|
25. |
24 |
10 |
0,5 |
|
26. |
25 |
5 |
1 |
|
27. |
26 |
5 |
3 |
|
28. |
25 |
3 |
2 |
|
29. |
28 |
3 |
2 |
|
30. |
25 |
2 |
4 |
|
31. |
27,29,30 |
10 |
0,5 |
|
32. |
31 |
10 |
0,5 |
|
33. |
32 |
7 |
1 |
|
34. |
32 |
2 |
1 |
|
35. |
33,34 |
10 |
1 |
На основе таблицы операций и карточки-определителя с учетом произведенной группировки параллельных операций осуществляется построение сетевого графика.
Сетевой график, пример
Определим критический путь. Критический путь на данном сетевом графике составляют операции: 1, 4, 5, 7, 8, 9, 13, 15, 16, 17, 18, 19, 24, 25, 28, 29, 31, 32, 33 (34), 35.
В результате построения сетевого графика работы можно сделать вывод, что деятельность организации не укладывается в заданный срок равный 22 рабочим дням, составляя вместо этого 26 дней. При этом операции первой, второй и третьей недели не укладываются в заданный для них срок, равный 5 рабочим дням. По сетевой модели операции 1 недели длятся 7 дней, 2 недели – 6 дней, 3 недели – 6 дней. Операции четвертой и пятой недель укладываются в заданные для них сроки.
Для соблюдения запланированных сроков произведем корректировку сетевого графика.
В нашем примере сетевого графика по данным карточки-распределителя можно сделать вывод, что для некоторых операций в рамках запланированных действий существует резерв специалистов в отделе. Учитывая, что общая численность сотрудников относительно невелика, можно воспользоваться способом корректировки сетевой модели с привлечением дополнительных ресурсов, в качестве которых выступают свободные на момент реализации операции специалисты данного отдела. Благодаря этому сократится срок выполнения операций критического пути, соответственно и сроки всей сетевой модели. Корректировке подлежат операции 1, 2 и 3 недель, так как операции 4 и 5 недель сетевого графика укладываются в заданные сроки.
После корректировки осуществим построение альтернативного сетевого графика.
Необходимо привлечь дополнительных специалистов для выполнения операций 4 (отдел специальных программ), 13 (отдел по организации оздоровительной кампании) и 18 (отдел специальных программ). Расчет трудоемкости операций (Q) определим исходя из произведения числа специалистов (N), выполняющих операцию, на число дней (t), выделенных для ее выполнения:
Q = N * t
Q4 = 2*4 = 8 ч/дн
Q13 = 2*3 = 6 ч/дн
Q18 = 2*2 = 4 ч/дн
В отделе специальных программ работает 5 человек, но в выполнении операции 4 задействовано только 2 человека. В результате привлечения двух специалистов новый срок выполнения операции составит: 8 / 4 = 2 дня. Следовательно, операция 4 будет выполняться 2 дня вместо 4 дней.
В отделе по организации оздоровительной кампании работает 3 специалиста, но в выполнении операции 13 занято только два человека. В данном случае привлечение одного дополнительного специалиста позволит сократить срок выполнения операции: 6 / 3 = 2 дня. Следовательно, операция 13 будет выполняться 2 дня вместо 3 дней.
В выполнении операции 18 задействовано 2 специалиста отдела специальных программ. Привлечение двух дополнительных специалистов позволит сократить срок ее выполнения: 4 / 4 = 1 день. Следовательно, операция 18 будет выполняться 1 день вместо 2 дней.
В результате получаем срок выполнения операций после корректировки сетевого графика с привлечением дополнительных ресурсов:
26 – 2 – 1 – 1 = 22 дня.
Таким образом, за счет произведенной коррекции сетевого графика срок выполнения операций, соответствует изначально заданному сроку в 22 рабочих дня.
Альтернативный график будет аналогичен предыдущему в плане своей структуры, корректировке подвергнуты сроки реализации операций согласно построенной сетевой модели.
Альтернативный сетевой график